《高等数学》课程教学资源（PPT课件）第八章向量代数与空间解析几何_第一节向量及其线性运算

第一节向量及其线性运算、向量的概念一向量的线性运算空间直角坐标系三四、利用坐标作向量的线性运算五、向量的模、方向角、投影返回MathGS公式数学家上页下页线与面

第一节 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影

第一节向量及其线性运算向量的概念一、向量：既有大小，又有方向的量称为向量，又称矢量表示法：有向线段M,M，或a.向量的模：向量的大小，记作M,Ml或Iαl.自由向量：与起点无关的向量，M2+P2单位向量：模为1的向量，记作e。零向量：模为0的向量，记作0PM返回MathGS公式上页下页线与面数学家

第一节 向量及其线性运算 M2 M1 P2 P1 自由向量: 表示法: 向量的模: 向量的大小， 向量: 既有大小，又有方向的量称为向量，又称矢量 与起点无关的向量． 单位向量: 模为1的向量， 零向量: 模为0的向量， 有向线段 M1M2 记作 e . 或 a． 一、向量的概念 记作 |M1M2 | 或 | a | . 记作 0

第一节向量及其线性运算相等：若向量a与b大小相等，方向相同，则称a与b相等，记作α=b．如图所示，MP2平行：若向量α与b方向相同或相反b1则称a与b平行，记作a/bPM规定：零向量与任何向量平行相等的两个向量负向量：与a大小相等，方向相反的向量称为α的负向量，记作一a.返回MathGS公式数学家上页下页线与面

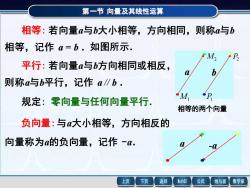
第一节 向量及其线性运算 相等: 若向量a与b大小相等，方向相同，则称a与b 相等，记作 a = b ． 平行: 若向量a与b方向相同或相反， 则称a与b平行，记作 a∥b ． 如图所示． 负向量:与a大小相等，方向相反的 向量称为a的负向量，记作 -a． 规定: 零向量与任何向量平行． a -a M2 M1 P2 P1 相等的两个向量 a b

第一节向量及其线性运算共线：因平行向量可以平移到同一直线上，故两向量平行又称两向量共线：共面：若k(k≥3)个向量经平移可移到同一平面上则称这k个向量共面.z0Q0不共面共线共面返回MathGS公式上页下页线与面数学家

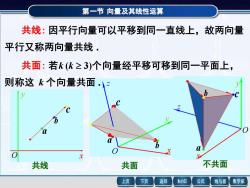
第一节 向量及其线性运算 x y z 共面 a b c O 共线: 因平行向量可以平移到同一直线上，故两向量 平行又称两向量共线 ． 共面: 若k (k  3)个向量经平移可移到同一平面上， 则称这 k 个向量共面 ． a b c x y 共线 O x y z 不共面 a b c O

第一节向量及其线性运算二、向量的线性运算1.向量的加法平行四边形法则：以α、b为邻边作平行四边形，该平行四边形的对角线即为和向量a+b，三角形法则：把b的起点移到a的终点，则以a的起点h为起点，以b的终点为b终点的向量即为和向-a量a+b .三角形法则平行四边形法则MathGS数学家上页下页返回公式线与面

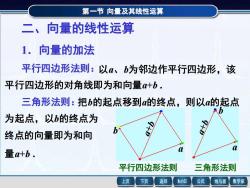
第一节 向量及其线性运算 平行四边形法则 三角形法则 a b a b 二、向量的线性运算 1．向量的加法 平行四边形法则：以a、b为邻边作平行四边形，该 平行四边形的对角线即为和向量a+b ． 三角形法则：把b的起点移到a的终点，则以a的起点 为起点，以b的终点为 终点的向量即为和向 量a+b ．

第一节向量及其线性运算运算规律交换律a+b=b+a.结合律a+(b+c)=(a+b)+c=a+b+c.运算规律的验证台三角形法则可以推广到多个向量相加的情形S如，s=a+b+c+d+ea返回MathGS公式数学家上页下页线与面

第一节 向量及其线性运算 运算规律 交换律 a + b = b + a . 结合律 a + (b + c) = (a + b ) + c = a + b + c . 第一节 向量及其线性运算 x o y z a a + b b b 求和向量的动态过程 运算规律的验证 三角形法则可以推广到多个向量相加的情形. 如，s=a+b+c+d+e a b c d e s

第一节向量及其线性运算2.向量的减法定义 b-a=b+(-a).显然，对于所有的向量，都有a+0=a,a-a=a+(-a)=0返回MathGS公式上页下页线与面数学家

第一节 向量及其线性运算 2．向量的减法 定义 b – a = b + (– a )． 显然，对于所有的向量 a ，都有 a + 0 = a ， a – a = a+ (– a ) = 0

第一节向量及其线性运算3.向量与数的乘法定义设k为一数，向量a与数k的乘积是一个新向量，记作ka。当k>0时，ka与a同向，且lka|=klal当k<0时，ka与a反向，且lka|=-klal当k=0时，ka=0.总之有|ka|=|klla|-2a2aMathGS上页下页返回公式线与面数学家

第一节 向量及其线性运算 3. 向量与数的乘法 定义 设 k 为一数，向量 a 与数 k 的乘积是一个 新向量，记作 ka . 当 k > 0 时，ka 与 a 同向，且 | ka | = k | a | ； 当 k < 0 时，ka 与 a 反向，且 | ka | = -k | a | ； 当 k = 0 时，ka = 0． 总之有 | ka | = | k | | a | ． a 2a -2a

第一节向量及其线性运算运算规律结合律(ua) = μu(la) = (au) a ;分配律(a+μ)a=aa+ua,a(a+b)=aa+ab.是一与同向的单位对于非零向量a，向量 e.向量，且a=ale。：这一过程称为把向量a单位化定理1非零向量，b平行的充要条件是，存在实数，使得b=a.证明包上页下页返回MathGS公式数学家线与面

第一节 向量及其线性运算 运算规律 结合律 (a) = (a) = ( ) a ； 分配律 ( + ) a =  a +  a ，  (a + b) =  a +  b ． 对于非零向量a，向量 | | . a a = a e 是一与a同向的单位 向量，且 a a ea | | 1 = 这一过程称为把向量a单位化． 定理1非零向量 a , b 平行的充要条件是，存在实数  ，使得 b =  a ． 第一节 向量及其线性运算 定理1 非零向量 a , b 平行的充要条件是，存在实数  ，使得 b =  a ． 证明 必要性 设 a 与 b 平行，取 , | | | | a b  =  当 a , b 同向时取正，反向时取负．则 b 与  a 同向，且 | | | |. | | | | | | | || | a b a b a =  a = = 使得 b =  a ． 再证唯一性．设又有b =  a ，则( -  )a = 0， 而 | a |  0 ，故 | -  | = 0，即  =  ．

第一节向量及其线性运算例1设α，b，c是3个任意的向量，若分别以0A，OB和 OC 表示.点P，Q，R，S分别是线段OA，AB,BC和 CD的中点．试分别求出OP,O0，OR，OS与a，b，c的关系式，从而推证 PQ=SR.R解包BSQP0A上页下页返回MathGS公式数学家线与面

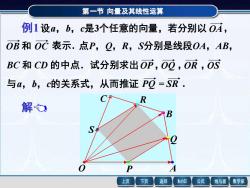
第一节 向量及其线性运算 例1 设a，b，c是3个任意的向量，若分别以 OA， OB 和 OC 表示．点P，Q，R，S分别是线段OA，AB， BC 和 CD 的中点．试分别求出OP，OQ ，OR ，OS 与a，b，c的关系式，从而推证 PQ = SR ． 第一节 向量及其线性运算 例1 设a，b，c是3个任意的向量，若分别以 OA， OB 和 OC 表示．点P，Q，R，S分别是线段OA，AB， BC 和 CD 的中点．试分别求出 OP，OQ ，OR ，OS 与a，b，c的关系式，从而推证 PQ = SR ． 解 O P A B C S Q R O P A B C S Q R