《高等数学》课程教学资源（PPT课件）第八章向量代数与空间解析几何_第五节曲面及其方程

第五节曲面及其方程曲面研究的基本问题旋转曲面三、柱面四、二次曲面五、高次代数曲面六、空间曲面欣赏返回MathGS公式上页下页线与面数学家

第五节 曲面及其方程 一、曲面研究的基本问题 二、旋转曲面 三、柱面 四、二次曲面 五、高次代数曲面 六、空间曲面欣赏

第五节曲面及其方程曲面研究的基本问题一、E在空间解析几何中，关于曲面的研究有下列两个基本问题：（1）已知一曲面作为点的几何轨迹时，求曲面方程2）已知方程时，研究它所表示的曲面的形状返回MathGS公式上页下页线与面数学家

第五节 曲面及其方程 一、曲面研究的基本问题 在空间解析几何中，关于曲面的研究有下列两个基 本问题： (1) 已知一曲面作为点的几何轨迹时,求曲面方程； (2) 已知方程时,研究它所表示的曲面的形状．

第五节曲面及其方程例1求动点到定点Mo(xo,yo,zo）距离为R的轨迹方程。解白例2 研究方程x2+y2+z2-2x+4y=0 表示怎样的曲面。解白如下形式的三元二次方程（A+0）A(x? + y? + z2)+ Dx+ Ey + Fz+G = 0都可通过配方研究它的图形上页下页返回MathGS公式数学家线与面

第五节 曲面及其方程 第五节 曲面及其方程 故所求方程为 M (x, y,z), 特别,当M0在原点时,球面方程为 解 设轨迹上动点为 , M0 M = R 即 依题意 ( ) ( ) ( ) . 2 0 2 0 2 x − x0 + y − y + z − z = R ( ) ( ) ( ) . 2 2 0 2 0 2 x − x0 + y − y + z − z = R . 2 2 2 2 x + y + z = R 例1 求动点到定点 ( , , ) 0 0 0 0 M x y z 方程. 距离为 R 的轨迹 M0 M x z O 例1 求动点到定点 方程. 距离为 R 的轨迹 例2 研究方程 的曲面. 表示怎样 第五节 曲面及其方程 解 例2 研究方程 2 4 0 2 2 2 x + y + z − x + y = 的曲面. 表示怎样 球心为 配方得 5 . (1, 2, 0), M0 − 可见此方程表示一个球面， 半径为 ( 1) ( 2) 5 . 2 2 2 x − + y + + z = x y z 如下形式的三元二次方程 ( A≠ 0 ) 都可通过配方研究它的图形

第五节曲面及其方程二、旋转曲面引例在MathGS中观察xOv面上的抛物线y=x?分别绕三条坐标和任意过原点的直线旋转而成的曲面xX7x7绕轴绕x轴绕y轴绕向量(1,1,1)动画包MathGS上页下页返回公式线与面数学家

第五节 曲面及其方程 二、旋转曲面 在MathGS中观察xOy面上的抛物线y=x 引例 2 分别 绕三条坐标和任意过原点的直线旋转而成的曲面． 绕x轴 x y z 绕y轴 x y z 绕z轴 x y z 绕向量(1,1,1) x y z 第五节 曲面及其方程 动画 绕x轴 绕z轴 绕y轴 绕向量

第五节曲面及其方程1.定义定义2一条平面曲线绕其平面上一条定直线旋转旋转曲面曲线称为旋转曲面一周所形成的曲面叫做门的母线，该定直线称为旋转轴旋转轴母线x旋转曲面返回MathGS下页公式线与面数学家上页

第五节 曲面及其方程 x y z 1. 定义 定义2 一条平面曲线绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面. 曲线称为旋转曲面 的母线， 母线 旋转轴 旋转曲面 该定直线称为旋转轴

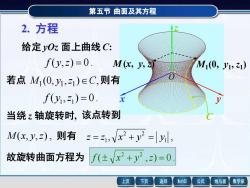
第五节 曲面及其方程2.方程Z给定yOz面上曲线C:f(y,z) = 0 .M(x, y, )Mi(0, Y1, z1)若点 M;(0,y1,z1) EC,则有f(y1,z)) =0 .xy当绕z轴旋转时，该点转到M(x,y,z)，则有z=21, Vx?+y2 =|yl,f(±x? +y2 ,2)=0故旋转曲面方程为下页返回MathGS公式数学家上页线与面

第五节 曲面及其方程 2. 方程 x y z M1 (0, y1 , z1 M (x, y, z) ) 故旋转曲面方程为 M (x, y,z) , 当绕 z 轴旋转时, ( , ) 0 . f y1 z1 = (0, , ) , 若点 M1 y1 z1 C 给定 yOz 面上曲线 C: , , 1 2 2 1 则有 z = z x + y = y ( , ) 0 . 2 2 f  x + y z = 则有 该点转到 f ( y,z) = 0 . C O

第五节曲面及其方程类似地，可求得yOz面上曲线C：f(y,z)=0，绕y轴旋转所得旋转曲面的方程为f(y,±x?+z?)=0f(x,±/y2+z2)=0f(x,y)=0，绕x轴曲线C：z=0绕y轴f(±Vx? +z?,J)=0f(x,±/y2 +z)=0f(x,z)=0, 绕x轴曲线C：y=0,绕轴f(±V/x? +y2,z)=0MathGS上页下页返回公式数学家线与面

第五节 曲面及其方程 yOz 面上曲线 C：f(y, z)=0，绕y轴旋转所得旋转曲面 类似地，可求得 的方程为 ( , ) 0 . 2 2 f y  x + z = 曲线 C：    = = 0 , ( , ) 0 , z f x y 绕x轴 ( , ) 0 , 2 2 f x  y + z = 绕y轴 ( , ) 0 , 2 2 f  x + z y = 曲线 C：    = = 0 , ( , ) 0 , y f x z 绕x轴 ( , ) 0 , 2 2 f x  y + z = 绕z轴 ( , ) 0 . 2 2 f  x + y z =

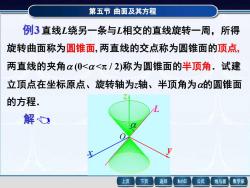
第五节曲面及其方程例3直线L绕另一条与L相交的直线旋转一周，所得旋转曲面称为圆锥面，两直线的交点称为圆锥面的顶点两直线的夹角α(0<α<元/2)称为圆锥面的半顶角．试建立顶点在坐标原点、旋转轴为z轴、半顶角为的圆锥面的方程.解包X返回MathGS公式数学家上页下页线与面

第五节 曲面及其方程 第五节 曲面及其方程 解 例3 直线L绕另一条与L相交的直线旋转一周，所得 旋转曲面称为圆锥面，两直线的交点称为圆锥面的顶点 两直线的夹角 (0< < / 2)称为圆锥面的半顶角．试建 立顶点在坐标原点、旋转轴为z轴、半顶角为的圆锥面 的方程． 直线L 的方程为 z = y cot . 绕 z 轴旋转时,圆锥面的方程为 cot , 2 2 z =  x + y  ( ) . 2 2 2 2 z = a x + y L  x y z O 例3 直线L绕另一条与L相交的直线旋转一周，所得 旋转曲面称为圆锥面, 两直线的交点称为圆锥面的顶点, 两直线的夹角 (0< < / 2)称为圆锥面的半顶角．试建 立顶点在坐标原点、旋转轴为z轴、半顶角为的圆锥面 的方程． L  x y z O

第五节曲面及其方程?例4求坐标面xOz上的双曲线=1分别绕x2Oa轴和z轴旋转一周所生成的旋转曲面方程解白例5如图所示的曲面称为圆环面，试建立其方程，并在MathGS中进行验证解白上页返回MathGS公式下页线与面数学家

第五节 曲面及其方程 例4 求坐标面 xOz 上的双曲线 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 第五节 曲面及其方程 例4 求坐标面 xOz 上的双曲线 1 2 2 2 2 − = c z a x 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 绕 x 轴旋转 1. 2 2 2 2 2 = + − c y z a x 解 所成曲面方程为 O z x y x y z 第五节 曲面及其方程 例5 如图所示的曲面称为圆环面，试建立其方程， x y z 解 并在MathGS中进行验证. 如图所示的圆环面是 由xOy面上的圆绕y轴旋转所成. 设圆的方程为 ( ) ( ) , 2 2 2 x − a + y −b = R 则圆环面的方程为 ( ) ( ) . 2 2 2 2 2 x + z − a + y −b = R 如图所示的圆环面参数a=b=2,R=0.5. x y z O 例5 如图所示的曲面称为圆环面，试建立其方程， 并在MathGS中进行验证

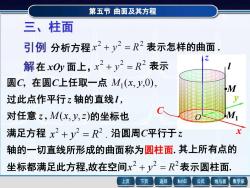
第五节 曲面及其方程三、柱面引例分析方程x2+2=R2表示怎样的曲面Z解在xOy面上，x2+2=R2表示圆C,在圆c上任取一点 M,(x,y,O)M过此点作平行z轴的直线l，V福M对任意 z，M(x,,z)的坐标也x满足方程x2+y=R2.沿圆周C平行于z其上所有点的轴的一切直线所形成的曲面称为圆柱面坐标都满足此方程,故在空间x2+y2= R2表示圆柱面.返回MathGS公式数学家上页下页线与面

第五节 曲面及其方程 引例 分析方程 表示怎样的曲面 . 的坐标也 在 xOy 面上， . 2 2 2 x + y = R 沿圆周C平行于 z 坐标都满足此方程,故在空间 2 2 2 x + y = R 轴的一切直线所形成的曲面称为圆柱面. 对任意 z , 过此点作平行 z 轴的直线l , 表示圆柱面. 圆C, ( , ,0), 1 M x y M (x, y,z) 其上所有点的 三、柱面 x y z M M1 满足方程 解 表示 在圆C上任取一点 l C O