《高等数学》课程教学资源（PPT课件）第八章向量代数与空间解析几何_第二节数量积、向量积、混合积

第二节数量积向量积混合积两向量的数量积两向量的向量积三、向量的混合积返回MathGS公式上页下页线与面数学家

第二节 数量积 向量积 *混合积 一、两向量的数量积 二、两向量的向量积 *三、向量的混合积

第二节数量积向量积混合积一、两向量的数量积引例设一物体在常力F的作用下作直线运动，位F移为s，力与位移的夹角为θ，如图所示则力所作的功为meSW =|Flls|coso在其他很多问题中，也会碰到对两个向量作相同的运算，因此需要对这种运算进行研究，上页下页返回MathGS公式数学家线与面

第二节 数量积 向量积 *混合积 一、两向量的数量积 引例 设一物体在常力 F 的作用下作直线运动，位 移为 s ，力与位移的夹角为，如图所示． F s 则力所作的功为  W =| F | | s| cos . 在其他很多问题中，也会碰到对两个向量作相同的 运算，因此需要对这种运算进行研究．

第二节数量积向量积混合积1.定义定义1对于任意两个向量a和b，称|alb|cose为ab与b的数量积，记作a·b，即0a·b=lallblcosea引例中功即为 W=F·S当向量a≠0 时，Prj.b=[blcosθ，故a· b=|a]Prjab同理，当b≠0时，有a·b=lbiPrjra.下页返回MathGS公式数学家上页线与面

第二节 数量积 向量积 *混合积 1. 定义 定义1 对于任意两个向量a和b，称| a | | b | cos 为a 与b的数量积，记作 a ·b ，即 a · b = | a | | b | cos  a b 引例中功即为 W = F s. 当向量a  0 时，Prjab = |b|cos ，故 a · b = | a | Prjab 同理，当 b  0 时，有 a · b = | b | Prjba ．

第二节数量积向量积混合积2.性质(1)a:a=|a|2 ;(2)a上b台a·b=03.运算规律(1)交换律 a·b=b·a;(2)结合律a (a·b)=(2a)·b=a·(2b) (3)分配律(a+b)·c=a·c+b·c.证明包下页返回MathGS公式数学家上页线与面

第二节 数量积 向量积 *混合积 2. 性质 (1) a · a = | a | 2 ； (2) a ⊥ b  a · b = 0． 3. 运算规律 (1) 交换律 a · b = b · a ； (2) 结合律  (a · b) = (a) · b = a · (b) ； (3) 分配律 (a + b) · c = a · c + b · c ． 第二节 数量积 向量积 混合积 证明 (1) 交换律 a ·b = b ·a ； (2) 结合律  (a ·b) = (a) ·b = a ·(b) ； (3) 分配律 (a + b) ·c = a ·c + b ·c ． 只证分配律．当 c = 0 时， a b c a + b Prjc a Prjc b Prjc (a+b) 显然成立， (a + b) ·c = | c | Prjc (a+b) = | c | (Prjc a + Prjc b) = | c | Prjc a + | c | Prjc b = a ·c + b ·c ． 当 c  0 时， 证毕

第二节数量积向量积混合积例1用向量的方法证明三角形的余弦定理，C解白baBA4.数量积的坐标表示C设 a=ai+aj+ak,b=bi+bj+bk，则a·b=(ai+aj+a.k).(bi+bj+b.k)=abi.i+abi.j+abi.k+a,bxj.i+a,b,j.j+a,b.j.k+abk.i+ab,k.j+a.b.k.kMathGS上页下页返回公式数学家线与面

第二节 数量积 向量积 *混合积 例1 用向量的方法证明三角形的余弦定理． 第二节 数量积 向量积 混合积 例1 用向量的方法证明三角形的余弦定理． 解 b a A c B C 对任意的ABC，令 AB = c ,CB = a ,CA= b . 则 c = a – b ． 从而有 c 2 = c ·c = (a – b) ·(a – b) = a ·a – 2a ·b + b ·b = | a | 2 + | b | 2 – 2 | a | | b | cosC ． 即 | c | 2 = | a |2 + | b |2 – 2 | a | | b | cosC . 余弦定理 4. 数量积的坐标表示 设 a i j k , b i j k , = ax + ay + az = bx + by + bz 则 a b ( i j k) ( i j k) ax ay az bx + by + bz  = + +  k i k j k k j i j j j k i i i j i k +  +  +  +  +  +  =  +  +  z x z y z z y x y y y z x x x y x z a b a b a b a b a b a b a b a b a b b a A c B C

第二节数量积向量积混合积a·b=(a,i+a,j+a.k).(bi+bj+b,k)=abi.i+abi.j+abi.k+a,bxj.i+a,b,j.j+a,b.j.k+a,b,k.i+a,b,k.j+a,b,k.k因为i.i=j.j=k.k=l,i.j=ji=j.k=k.j=k.i=i.k=0因此得到两向量的数量积的坐标计算公式a.b=ab+a,b,+a.bMathGS上页下页返回公式线与面数学家

第二节 数量积 向量积 *混合积 因为 i i = j  j = k k =1, i  j = j i = j k = k  j = k i = i k = 0 , 因此得到两向量的数量积的坐标计算公式 . x x y y z z a b = a b + a b + a b a b ( i j k) ( i j k) ax ay az bx + by + bz  = + +  k i k j k k j i j j j k i i i j i k +  +  +  +  +  +  =  +  +  z x z y z z y x y y y z x x x y x z a b a b a b a b a b a b a b a b a b

第二节数量积向量积混合积由数量积的定义和坐标计算公式，还可得到两非零向量夹角的计算公式，设向量a，b均为非零向量a·b=|allb|cos0a.bcosO:[a| b]ab+a,b,+a.bcOseVa?+a+a?yb?+b+bMathGS返回公式数学家上页下页线与面

第二节 数量积 向量积 *混合积 由数量积的定义和坐标计算公式，还可得到两非零 向量夹角的计算公式． 设向量 a，b 均为非零向量 a b =| a | | b | cos , , | | | | cos a b a b  = cos . 2 2 2 2 2 2 x y z x y z x x y y z z a a a b b b a b a b a b + + + + + +  =

第二节数量积向量积混合积例2 已知三点M(1,1, 1), A(2, 2, 1)和B(2, 1, 2)，求ZAMB.B解台hMAa例3设a+b+c=0，a|=1,{b|=2，lc|=3,求a·b+b·c+c·a.解台下页返回MathGS公式数学家上页线与面

第二节 数量积 向量积 *混合积 例2 已知三点M(1, 1, 1), A(2, 2, 1)和B(2, 1, 2)，求 第二节 数量积 向量积 混合积 解 a b M A B 令 例2 已知三点M(1, 1, 1), A(2, 2, 1)和B(2, 1, 2)，求 AMB ． a = MA, b = MB , 则 a = (1, 1, 0), b = (1, 0, 1)． , 2 1 | | | | cos =   = a b a b AMB 所以 . 3 π AMB = AMB ． 例3 设 a + b + c = 0，| a | = 1， | b | = 2， | c | = 3， 第二节 数量积 向量积 混合积 解 例3 设 a + b + c = 0，| a | = 1， | b | = 2， | c | = 3， 求 a ·b + b ·c + c ·a ． a + b + c = 0 , (a + b + c) 2 = 0 , a ·a + b ·b + c ·c + 2a ·b + 2b ·c + 2c ·a = 0 , | a | 2 + | b | 2 + | c | 2 + 2a ·b + 2b ·c + 2c ·a = 0 , 故 a ·b + b ·c + c ·a = -7． 求 a · b + b · c + c · a ． a b M A B

第二节数量积向量积混合积二、两向量的向量积引例设0为一根杠杆的支点，有一个力F作用于这F杠杆上的P点处，F与杠杆的夹角为LP0鱼力学规定，力F对支点O的力矩是金a一向量M，它的模|M=|OPF|sinθ'Q而它的方向垂直于OP与F所决定的平面，指向是按右手规则从OP以不超过元的角转向F来确定上页下页返回MathGS公式数学家线与面

第二节 数量积 向量积 *混合积 二、两向量的向量积 引例 设O为一根杠杆的支点，有一个力 F 作用于这 杠杆上的P点处，F 与杠杆的夹角为 ． O L F P  Q 由力学规定，力F 对支点O的力矩是 一向量M，它的模 | M |=|OP | | F |sin  . 而它的方向垂直于 OP 与F 所决定的平面，指向是按右 手规则从 OP 以不超过  的角转向F 来确定．

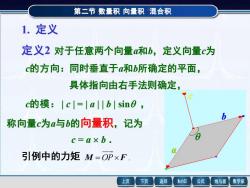
第二节数量积向量积混合积1. 定义定义2对于任意两个向量a和b，定义向量c为c的方向：同时垂直于a和b所确定的平面具体指向由右手法则确定c的模：「c{=「ab「sin，b称向量c为a与b的向量积，记为c=axb.引例中的力矩 M=OP×F.返回MathGS上页下页公式线与面数学家

第二节 数量积 向量积 *混合积 a b c  1. 定义 定义2 对于任意两个向量a和b，定义向量c为 c的模： | c | = | a | | b | sin ， c的方向：同时垂直于a和b所确定的平面， 具体指向由右手法则确定， 称向量c为a与b的向量积，记为 c = a  b ． 引例中的力矩 M = OPF