《高等数学》课程教学资源（课件讲稿）第五章课件_第五章第三节广义积分

第五章第三节广义积分积分限有限定积分被积函数有界推广反常积分（广义积分）、无穷区间上的广义积分无界函数的广义积分HIGH EDUCATION PRESS下页返回结束机动目录上页

二、无界函数的广义积分 第三节 定积分 积分限有限 被积函数有界 推广 一、无穷区间上的广义积分 机动 目录 上页 下页 返回 结束 反常积分 (广义积分) 广义积分 第五章

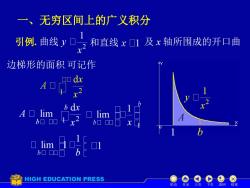
一、无穷区间上的广义积分引例。曲线y和直线x1及x轴所围成的开口曲边梯形的面积可记作广dxAOLCdx580A lim lim.2o口bB%E 01limbooHIGH EDUCATION PRESS下页返回结束机动目录上页

一、无穷区间上的广义积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 可记作 机动 目录 上页 下页 返回 结束

定义l.设f(x)C[a,),取b a,若blimf(x)dxHb存在，则称此极限为f(x)的无穷限广义积分，记作bf(x)dx limf(x)dx0boo这时称反常积分f(x)dx收敛；如果上述极限不存在口Of(x)dx发散就称反常积分C类似地，若f(x)C(,b]，则定义6hf(x)dxf(x)dx limaoHIGHEDUCATION PRESS上页下页返回结束机动目录

定义1. 设 若 存在 , 则称此极限为 f (x) 的无穷限广义积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 则定义 机动 目录 上页 下页 返回 结束

若f(x)□C(，□□)，则定义f(x)dx E limf(x)dx limf (x)dxb a（c为任意取定的常数）只要有一个极限不存在，就称f(x)dx 发散HIGH EDUCATION PRESS上页下页返回结束机动目录

则定义 ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 机动 目录 上页 下页 返回 结束

若F(x)是f(x)的原函数，引入记号F() lim F(x); F() lim F(x)x口x口则有类似牛一莱公式的计算表达式f (x)dx F(x)F() F(a)bf(x)dx F(x)F(b) F()f(x)dx F(x)F（)F（)HIGH EDUCATION PRESS上页下页返回结束机动目录

引入记号 则有类似牛 – 莱公式的计算表达式 : 机动 目录 上页 下页 返回 结束

dx9例1.计算广义积分01xdx解：[arctan x10x1x二xdxXo对吗?思考:xxdx分析：noDr原积分发散！HIGH EDUCATION PRESS返回结束机动目录上页下页

例1. 计算广义积分 解: 机动 目录 上页 下页 返回 结束 思考: 分析: 原积分发散 !

dx当p>1 时收敛；p≤l例2.证明第一类p积分rp时发散证：当p=1 时有dxih当p1时有p 1dxlOpp lDDUD因此,当p>1时，广义积分收敛，其值为口1当p≤l 时,广义积分发散HIGH EDUCATION PRESS上页下页返回结束机动目录

例2. 证明第一类 p 积分 证:当 p =1 时有 当 p ≠ 1 时有 当 p >1 时收敛 ; p≤1 时发散 . 因此, 当 p >1 时, 广义积分收敛 , 其值为 当 p≤1 时, 广义积分发散 . 机动 目录 上页 下页 返回 结束

101dt (p O)例3.计算广义积分解：原式eptJptdt00nDpte20pDHIGHEDUCATION PRESS下页返回结束机动目录上页

例3. 计算广义积分 解: 机动 目录 上页 下页 返回 结束

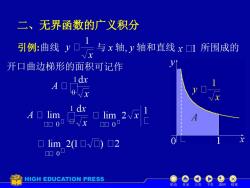
二、无界函数的广义积分引例：曲线y与x轴,轴和直线x1所围成的开口曲边梯形的面积可记作1dxAOL0Xdx1A lim lim 22VxA品x吕 lim_2(1 V) □2日HIGH EDUCATION PRESS上页下页返回结束机动目录

二、无界函数的广义积分 引例:曲线 与 x 轴, y 轴和直线 所围成的 开口曲边梯形的面积可记作 机动 目录 上页 下页 返回 结束

定义2. 设 f(x)C(a,b]l,而在点α的右邻域内无界取口O，若极限lim-f(x)dx存在，则称此极限为函000数f(x)在[α，b]上的广义积分,记作hhf(x)dxf(x)dx lim00b口f(x)dx 收敛；如果上述极限不存在这时称广义积分bf(x)dx 发散就称广义积分类似地,若 f(x)C[a,b),而在 b的左邻域内无界6b则定义f(x)dxf(x)dx limHIGH EDUCATION PRESS上页下页返回结束机动目录

定义2. 设 而在点 a 的右邻域内无界, 存在 , 这时称广义积分 收敛 ; 如果上述极限不存在, 就称广义积分 发散 . 类似地 , 若 而在 b 的左邻域内无界, 若极限 数 f (x) 在 [a , b] 上的广义积分, 记作 则定义 机动 目录 上页 下页 返回 结束 则称此极限为函