《高等数学》课程教学资源（课件讲稿）第五章 定积分_5-3 定积分的换元法与分部积分法

第三节第五章定积分的换元法和分部积分法不定积分换元积分法换元积分法→定积分分部积分法分部积分法一、定积分的换元法二、定积分的分部积分法

二、定积分的分部积分法 第三节 不定积分 一、定积分的换元法 换元积分法 分部积分法 定积分 换元积分法 分部积分法 定积分的换元法和 分部积分法 第五章

一、定积分的换元法定理1.设函数f(x)eC[a,b],单值函数x=p(t)满足1) p(t)eC'[α, β], (α)= a, p(β)= b;2)在[α,β 上a≤p(t)≤b,[~ f(x)dx =f f [g(0)]p'(t) dt则证：所证等式两边被积函数都连续，因此积分都存在且它们的原函数也存在.设Fx）是f(x）的一个原函数则F[(t)]是f[g(t)]p(t)的原函数，因此有(~ f(x)dx= F(b)- F(a)= F[p(β)) - F[(α))f [o(t)]p'(t)dt

一、定积分的换元法 定理1. 设函数 单值函数 满足: 1) ( ) [ , ], 1  t C   2) 在 [ ,  ] 上 ( )  a , ( )  b; (t) (t) 证: 所证等式两边被积函数都连续, 因此积分都存在 , 且它们的原函数也存在 . 则 是 的原函数 , 因此有  F(b)  F(a)  F[( )]  F[()] (t) (t) (t) (t) (t) 则

[ f(x)dx =fβ f [o(0)]p'(t) dt说明：1)当β<α，即区间换为[β,α|时，定理1仍成立2）必需注意换元必换限，原函数中的变量不必代回3）换元公式也可反过来使用，即P f[p(t)]p'(t) dt= [~ f(x)dx (令x= p(t))或配元fLp(t) J'(t) dt = fp f[ p(t) 1 d p(t)配元不换限

说明: 1) 当 <  , 即区间换为 [ ,]时， 定理 1 仍成立 . 2) 必需注意换元必换限 , 原函数中的变量不必代回 . 3) 换元公式也可反过来使用 , 即 f x x (令 x  (t)) b a ( )d   或配元 (t) d(t) 配元不换限 (t) (t) (t) (t) (t) (t)

Va? - x? dx (a>0).例1.计算解：令x=asint，则dx=acostdt，且当x=0时,t=0; x=α时,t=．原式=α2cos2tdtyt y=Na?-x?(+cos21)dtS元12元asin2t又

例1. 计算 解: 令 x  a sin t , 则 dx  a cost d t , 当 x  0时, t  0; , . 2 π x  a 时 t  ∴ 原式 = 2 a t t a (1 cos 2 )d 2 2 π 0 2    sin 2 ) 2 1 ( 2 2 t t a   0 2 π  2 π 0 cos t d t 2 O 2 2 y  a  x x y a 且

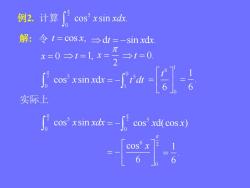
例2.计算 cos' x sin xdx.解: 令 t = cosx, →dt=-sin xdx.元=t=0x=0=t=1x=2I' o xind - ra [ -实际上cos x sin xdx = -cos' xd(cos x)-[-

2 5 0 cos sin . x xdx   解: 令 t x  cos ,    d sin d . t x x 2 x  x  0  t 1,   t 0. 2 5 0 cos sin d x x x   0 5 1   t dt  1 6 0 6   t      1 . 6  例2. 计算 实际上 2 5 0 cos sin x xdx   2 5 0 cos d(cos ) x x    6 2 0 cos 6 x          1 . 6 

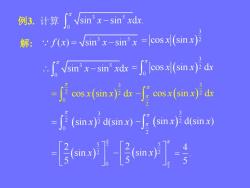
Vsin"x-sin'xdx.例3.计算解: : f(x)= /sin' x-sin'x =|cosx(sinx)2S* Vsin' x-sin' xdx = f" Icos xl(sin x)2 dxJe cos x(sin x) dx -J= cos x(sin x) dx (sinx) d(sin x) -[ (sin x) d(sin x)[(sin)][,(sin)]-

例3. 计算 3 5 0 sin sin d . x x x    解: 3 5 f x x x ( ) sin sin     3  cos sin x x 2 3 5 0 sin sin d x x x       3 2 0 cos sin d x x x      3 2 2 0 cos sin d x x x      3 2 2 cos sin d x x x     3 2 2 0 sin d(sin ) x x      3 2 2 sin d(sin ) x x     5 2 2 0 2 sin 5 x           2 5 2 2 sin 5 x          4 . 5 

larcsinx练习．计算dx/x(1 -x)

练习. 计算 1 0 arcsin d . (1 ) x x x x  

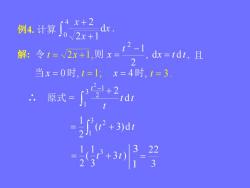
4x+2dx例4.计算J0/2x+1t2-解：令t=~2x+1,则x=dx=tdt, 且2当x=0时,t=1:x=4时,t=3原式=tdt=(c2+3)d223+3t)3

例4. 计算 解: 令 t  2x 1, 则 , d d , 2 1 2 x t t t x    当 x  0时, x  4时, t  3 . ∴ 原式 = t t t t d 3 2 1 2 1 2    (t 3) d t 2 1 3 1 2    3 ) 3 1 ( 2 1 3  t  t 1 3 t  1; 且

偶倍奇零例5. 设 f(x)eC[-a,a],(1)若f(-x)= f(x), 则[~ f(x)dx=2f~f(x)dx(2)若f(-x)=-f(x), 则(α f(x)dx = 0证: [° f(x)dx = [° (x)dx + Jf(x)dx令x=-1= J°f(-t)dt + f°f(x)dxJ°l f(-x)+ f(x)]dx2f°f(x)dx, f(-x)= f(x)时0f(-x)=-f(x)时

例5. 证: (1) 若     a a a f x x f x x 0 则 ( ) d 2 ( ) d   f x x aa ( ) d (2) 若 ( ) d  0 aa 则 f x x f x x a ( ) d 0  f x x a ( ) d 0   f t t a ( ) d 0    f x x a ( )d 0   f x f x x a[ ( ) ( )]d 0     f (x)  f (x)时 f (x)   f (x)时 偶倍奇零 令 x   t 

例6. 设 f(x)eC[0,1],证明(1) 2 f(sin x)dx =f2 f(cos x)dx ;(2) (sinx)dx=号J。f(sinx)dx,由此计算xsinxdx.O1+cos?x元证明：(1)设x=t =dx=-dt.2元元x=0=t=t=0X2[sn(-)[’ f(sin x)dx = -]dt= f" f(cost)dt = I" f(cos x)dx;

例6. (1) (2) (1) 设 2 x t       dx dt, x  0 , 2 t    2 x    t 0. 2 0 f x dx (sin )   2 0 sin 2 f t dt                   2 0 f t dt (cos )    2 0 f x dx (cos ) ;    证明：