《高等数学》课程教学资源（课件讲稿）第五章 定积分_5-1 定积分的概念与性质

第五章第一节定积分的概念及性质一、定积分问题举例二、 定积分的定义三、 定积分的性质

第一节 一、定积分问题举例 二、 定积分的定义 定积分的概念及性质 第五章 三、 定积分的性质

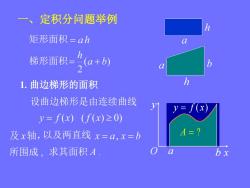
一、定积分问题举例矩形面积=ahh梯形面积==(α+b)b2h1.曲边梯形的面积设曲边梯形是由连续曲线Vy= f(x)y=f(x) (f(x)≥0)A=?及x轴，以及两直线x=α,x=b所围成，求其面积AbxC

一、定积分问题举例 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . A  ? y  f (x) 矩形面积 梯形面积 y O a b x

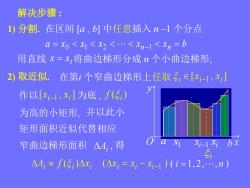
解决步骤：1)分割.在区间[a,b]中任意插入n-1个分点α = Xo <Xj < X2 <... < Xn-1 <xn = b用直线x=x将曲边梯形分成n个小曲边梯形2取近似．在第i个窄曲边梯形上任取SiE[xi-1，xi]V作以[xi-1,x,l为底，f()为高的小矩形，并以此小矩形面积近似代替相应Oaxixi-ixibx窄曲边梯形面积 △Ai，得SiAA, = f(5)Axi(△x, = x; -Xi-1)(i=1,2,..,n)

1x i x i1 a x y O 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a x x x x x b  0  1  2    n1  n  [ , ] i i 1 i x x    用直线 i x  x 将曲边梯形分成 n 个小曲边梯形; 2) 取近似. 在第i 个窄曲边梯形上任取 作以 [ , ] i 1 i x x  为底 , ( ) i f  为高的小矩形, 并以此小 矩形面积近似代替相应 窄曲边梯形面积 得 ( ) ( )  i  i  i  i  i  i1 A f  x x x x i

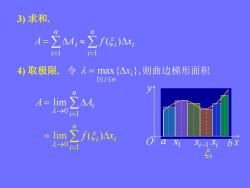
3)求和。A=A;~f(Ei)Axii=1i14)取极限。令=max△x，则曲边梯形面积<i≤nnAAA= lim2-0i=1nlimEf(E)AxioaxiXi-1 Xibx10i-15i

3) 求和.     n i A Ai 1     n i i i f x 1 ( ) 4) 取极限. 令 则曲边梯形面积      n i A Ai 1 0 lim       n i i i f x 1 0 lim ( )  1x i x i1 a x y O i

2.变速直线运动的路程设某物体作直线运动,已知速度 =v(t)εC[T,T2],且v(t)≥0，求在运动时间内物体所经过的路程s解决步骤：1)分割。在[T,T2]中任意插入n-1个分点,将它分成n个小段[ti-1,ti;](i=l,2,,n),在每个小段上物体经过的路程为 △s;(i=l,2,,n)2）取近似。任取;E[ti-1,til,，以v(Si)代替变速，得As, =v(5)At (i=1, 2,.,n)

2. 变速直线运动的路程 设某物体作直线运动, 且 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 分割. 将它分成 在每个小段上物体经 2) 取近似. 得 i i i  s  v( )t (i  1, 2,  , n) 已知速度 n 个小段 过的路程为

3)求和。v(6i)Ati2i-l4）取极限.ns = lim(a = max △t)Cv(Ei)Ati20日<i<n上述两个问题的共性·解决问题的方法步骤相同“分割，取近似，求和，取极限·所求量极限结构式相同：特殊乘积和式的极限

3) 求和. 4) 取极限 . 上述两个问题的共性: • 解决问题的方法步骤相同 : “分割 , 取近似 , 求和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限

二、定积分定义(P226)设函数f(x)定义在[a,b]上有界，在[a，b]中任意插入若干个分点a = Xo<i<X2<...<xn = b,把区间[a,b]分成n个小区间[xo,x],[x,x,],,[x,x,],.".,[x-1,xn]各个小区间的长度依次为Ax = xi - Xo,Ax, = X2 -Xi,"-,Ax, = x, - xi-1,""-,Ax, = x, - xn-1在每个小区间[xi-,x]上任取一点（x-≤≤x),作函数值f（）与小区间长度△x的乘积f（5）△x（i=1,2n）并作出和S=Zf(5)Ax,i=1

二、定积分定义 (P226 ) , 0 1 2 a x x x x b       n 

记=max△x,Ax,,△x,….,Ax,，如果当→0时1<i≤n这和的极限总存在，且与闭区间α,b的分法及点三的取法无关，则称此极限I为函数fx）在区间[a，b]上的定积分，记作f(x)dxnZf(5)Ax;即f(x)dx=lim2→0-1此时称f(x）在［α，b］上可积

则称此极限 I 为函数 在区间 上的定积分,  b a f (x) dx 即   b a f (x) dx i n i i  f x  1 0 lim ( )  此时称 f ( x ) 在 [ a , b ] 上可积 . 记作

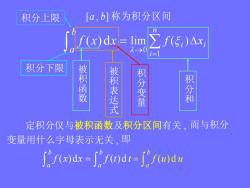
[a,b]称为积分区间积分上限nFZf(5)Ax;f(x)dx= lim10i=1积分下限被积函数被积表达式积分变量积分和定积分仅与被积函数及积分区间有关，而与积分变量用什么字母表示无关，即["f(x)dx=f"f(t)dt=f"f(u)du

  b a f (x) dx i n i i  f x   1 0 lim ( )  积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 [a , b] 称为积分区间 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即  b a f (x) dx   b a f (t) d t   b a f (u) d u

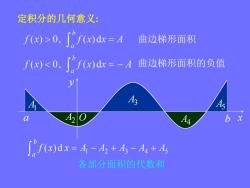
定积分的几何意义：f(x)>0, (~f(x)dx = A曲边梯形面积f(x)<0，~f(x)dx=-A 曲边梯形面积的负值A5AbxC[° f(x)dx = A - A2 + As - A4 + As各部分面积的代数和

定积分的几何意义: 曲边梯形面积 曲边梯形面积的负值 a b y x A1 A2 A3 A4 A5 1 2 3 4 5 f (x) d x A A A A A b a       各部分面积的代数和 O