《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-2 换元积分法

第四章第二节换元积分法一、第一类换元法二、第二类换元法
二、第二类换元法 第二节 一、第一类换元法 换元积分法 第四章

基本思路设F'(u)=f(u),u=β(x)可导,则有dF[o(x)= f[0(x)lo'(x)dx[ f[p(x)]p'(x)dx =F[0(x)]+ C = F(u)+ Cu=(x)=J f(u)du|u=g(x)第一类换元法J f(u)du[ [(x)]g'(x)dx第二类换元法
第二类换元法 第一类换元法 基本思路 设 F (u ) f (u ) , 可导, F [ ( x ) ] C ( ) ( )d u x f u u ( ) ( ) C u x F u dF [ ( x ) ] f [ ( x ) ] ( x )d x 则有

一、第一类换元法定理1.设f(u)有原函数,u= (x)可导,则有换元公式J f[o(x)]p(x)dx =J f(u)duu= p(x)即[ f[o(x)]p'(x)dx = f(o(x)d p(x)(也称微分法)
一、第一类换元法 定理1. 设 f (u ) 有原函数 , u ( x ) 可 导 , 则有换元 公式 f (u)du u ( x ) f ( ( x) )d ( x) (也称 即 f [ ( x ) ] ( x )dx 凑微分法)

注:(f[p(x)lo'(x)dx由定理可见,虽然是一整体记号,但可把dx视为自变量微分→[ f[d(x)]p(x)dx=[ [p(x)dp(x) 一—凑微分u=p(x)[ f(u)du——换元[F(u)+C], u=e(x) 一一回代=F[p(x)]+C步骤:凑微分;换元求出积分;回代原变量
注: dx 由定理可见,虽然 f x x x [ ( )] ( )d 是一整体记号,但可把 视为自变量微分 f x f x [ ( )] [ ( ) ( )d d ) x x ] (x ——凑微分 步骤: 凑微分;换元求出积分;回代原变量 u x ( ) f u u ( )d ——换元 F u C ( ) ( ) u x F x C [ ( )] ——回代

例1.求「sin 2 xdx.解:(sin2xdxsin2x-(2x)'dx---凑微分sin2xd(2x)令u=2xsinudu ----换元cosu+C2u=2xcos(2x)+C--回代原变量2
例1. 求 sin 2 d . x x 解: sin 2 dx x sin 2 d x x (2 ) x 1 2 1 sin 2 d(2 ) 2 x x 令u x 2 1 sin d 2 u u 1 cos 2 u C 2 u x 1 cos(2 ) . 2 x C -凑微分 -换元 -回代原变量
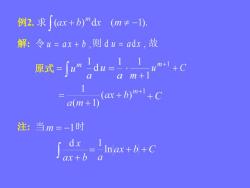
例2.求[(ax+b)"dx (m±-1).解:令u=ax+b,则du=adx,故m+1lumidu原式=「福m+1Q(ax + b)m+1 + Ca(m+1)注:当m=-1时dx=- inlax+bl+Cax+bC
例2. 求 解: 令 u a x b , 则 d u a d x , 故 原式 = m u u a d 1 a 1 u C m m 1 1 1 注: 当 时

例3.求dx(x+2)解:令u=x+2,则x=u-2,dx= du.于是(u-2)2dx-du=[ (u? - 4u + 4)u-" dux+2)[(u-" - 4u-? + 4u-3)du=ln |ul + 4u-l - 2u-2 + C2=lnx+2|+x+2(x+2)
例3. 求 解:

dx想到公式例4.求dudxdx解:l+u= arctan u +u=则du=dxarctanu+caarctan(=)+ Ca
2 2 1 d 1 ( ) xax a 例4. 求 解 : , ax 令 u 则 x a u d 1 d 2 1 u d u a1 u C a arctan 1 想到公式 2 1 d uu a r c t a n u C ( ) xa

dx例5.求(a> 0).d()dxdx解:1-()2一=arcsin=+Cadu想到arcsinu+CJ [o(x)o'(x)dx = [ f(o(x)dp(x)(直接凑微分)
例5. 求 2 1 d u u 想到 a r c s i n u C 解: 2 d 1 ( ) x a x a f ( ( x) )d ( x) (直接凑微分) f [ ( x ) ] ( x )dx 2 d( ) 1 ( ) x a x a
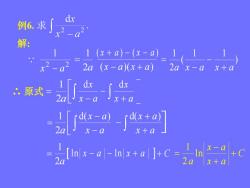
dx例6.求解:1(x+a)-(x-a) 1(2a(x-a)(x+a))2ax-ax+a[- da:原式c+a-2[-[ a]x+ax-a_[1n|x-a|-In|x+al ]+C =_in2ax+a
C x a x a a ln 2 1 例6. 求 解: 2 2 1 x a (x a)(x a) ( x a ) ( x a ) 2a 1 ) 1 1 ( 2 1 a x a x a ∴ 原式 = 2a 1 x a x x a dx d 2a 1 x a d(x a) 2a 1 ln x a l n x a C x a d(x a)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-5 函数的微分.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-4 隐函数和参数方程求导及相关变化率.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-3 高阶导数.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-2 求导法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-1 导数概念.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-7 曲率.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-6 函数图形的描绘.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-5 函数的极值与最大值最小值.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-4 函数的单调性与曲线的凸凹性.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-3 泰勒公式.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-2 洛必达法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-1 微分中值定理.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-9 连续函数的运算与初等函数的连续性.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-8 函数的连续性与间断点.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-7 无穷小比较.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-6极限存在准则 两个重要极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-5 极限运算法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-4 无穷小与无穷大.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-3 函数极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-2 数列极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-3 分部积分法.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-4 有理函数的积分.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-1 微分方程的基本概念.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-2 可分离变量微分方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-3 齐次方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-4 一阶线性微分方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-5 可降阶高阶微分方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-6 高阶线性微分方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-7 常系数齐次线性微分方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-8 常系数非齐次线性微分方程.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章 定积分_5-1 定积分的概念与性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章 定积分_5-2 微积分基本公式.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章 定积分_5-3 定积分的换元法与分部积分法.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章 定积分_5-4 反常积分.pdf
- 《高等数学》课程教学资源(课件讲稿)第六章 定积分的应用_6-1 定积分的元素法.pdf
- 《高等数学》课程教学资源(课件讲稿)第六章 定积分的应用_6-2 定积分在几何学上的应用.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-1 不定积分的概念与性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章课件_第三章第一节.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章课件_第三章第三节.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章课件_第三章第二节.pdf
