《高等数学》课程教学资源（PPT课件）第九章多元函数微分法及其应用_第一节多元函数的基本概念

第一节多元函数的基本概念平面点集多元函数概念三、多元函数的极限四、多元函数的连续性返回MathGS公式上页下页线与面数学家

第一节 多元函数的基本概念 一、平面点集 二、多元函数概念 三、多元函数的极限 四、多元函数的连续性

第一节多元函数的基本概念一、平面点集1.邻域设Po(xo,Jo)是xOy平面上的一个点，是某一正数,与点Po(xo,yo)距离小于S的点P(x,J)的全体，称为点Po的S邻域，记作U(P。，)，即U(P,)=(PIIPP<S) :也就是U(P,) =((x, y)/ /(x-xo)? +(y-yo)? <S)返回MathGS公式数学家上页下页线与面

第一节 多元函数的基本概念 一、平面点集 1. 邻域 设P0 (x0 , y0 )是xOy平面上的一个点，是某一正数， 与点P0 (x0 , y0 )距离小于 的点P(x , y)的全体，称为点P0 的 邻域，记作 U(P0 ,  )，即 ( , ) { | | | }, U P0  = P PP0   也就是 ( , ) {( , )| ( ) ( ) }. 2 0 2 U P0  = x y x − x0 + y − y 

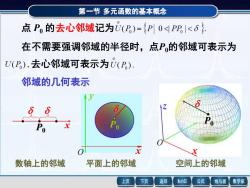
第一节多元函数的基本概念点P。的去心邻域记为(P)={P0PP<在不需要强调邻域的半径时，点P.的邻域可表示为U(P），去心邻域可表示为U(P）邻域的几何表示SZ8d9PPo十POx0x空间上的邻域数轴上的邻域平面上的邻域MathGS上页下页返回公式线与面数学家

第一节 多元函数的基本概念 点 P0 的去心邻域记为 在不需要强调邻域的半径时，点P0的邻域可表示为 去心邻域可表示为 邻域的几何表示 P0  O x y 平面上的邻域 x 数轴上的邻域 P0   P0 x z 空间上的邻域  O

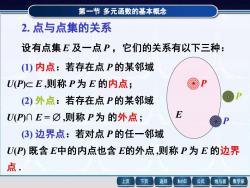
第一节多元函数的基本概念2.点与点集的关系设有点集E及一点P，它们的关系有以下三种(1)内点：若存在点P的某邻域U(P)CE,则称P为E的内点(2)外点：若存在点P的某邻域EU(P)N E=の ,则称 P为 的外点P(3)边界点：若对点P的任一邻域U(P既含E中的内点也含E的外点,则称P为E的边界点下页返回MathGS公式上页线与面数学家

第一节 多元函数的基本概念 E 2. 点与点集的关系 设有点集 E 及一点 P ，它们的关系有以下三种： (1) 内点：若存在点 P 的某邻域 (2) 外点：若存在点 P 的某邻域 (3) 边界点：若对点 P 的任一邻域 U(P) E ,则称 P 为 E 的内点； U(P)∩ E =  ,则称 P 为 的外点 ; U(P) 既含 E中的内点也含 E的外点 ,则称 P 为 E 的边界 点 . P P P

第一节多元函数的基本概念E的边界点的全体，称为E的边界，记作aE，由定义可知，E的内点一定属于E，E的外点一定不属于E，E的边界点可能属于E，也可能不属于E聚点：如果对于任意给定的正数8，点P的去心邻域ü(P。,S）内总有E中的点，则称P是E的聚点聚点可以属于E，也可以不属于E（因为聚点可以为E的边界点）MathGS上页下页返回公式线与面数学家

第一节 多元函数的基本概念 E的边界点的全体，称为E的边界，记作 E . 由定义可知，E的内点一定属于E，E的外点一定不 属于E，E的边界点可能属于E，也可能不属于E． 聚点： 如果对于任意给定的正数 ，点 P 的去心邻 域 内总有E中的点，则称P是E的聚点． 聚点可以属于 E , 也可以不属于E (因为聚点可以为 E 的边界点)．

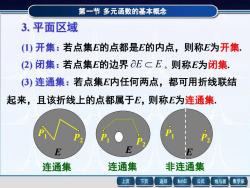
第一节多元函数的基本概念3.平面区域(1)开集：若点集E的点都是E的内点，则称E为开集(2)闭集：若点集E的边界aECE，则称E为闭集(3）连通集：若点集E内任何两点，都可用折线联结起来，且该折线上的点都属于E，则称E为连通集.PPBP2PPEEE连通集非连通集连通集返回MathGS公式上页下页线与面数学家

第一节 多元函数的基本概念 3. 平面区域 (1) 开集：若点集E的点都是E的内点，则称E为开集. (2) 闭集：若点集E的边界 E  E , 则称E为闭集. (3) 连通集：若点集E内任何两点，都可用折线联结 起来，且该折线上的点都属于E，则称E为连通集. E P1 P2 E P1 P2 E P1 P2 连通集 连通集 非连通集

第一节多元函数的基本概念(4)区域(或开区域）：连通的开集称为区域或开区域(5）闭区域：开区域同它的边界一起所构成的点集称为闭区域(6)有界集：对于平面点集E，如果存在某一正数r,使得EcU(O,r)其中O是坐标原点，则称E为有界集(7）无界集：一个集合如果不是有界集，就称这集合为无界集返回MathGS公式数学家上页下页线与面

第一节 多元函数的基本概念 (4) 区域(或开区域)：连通的开集称为区域或开区域. (5) 闭区域：开区域同它的边界一起所构成的点集称 为闭区域. (6) 有界集：对于平面点集E，如果存在某一正数 r， 使得 E  U(O , r) , 其中O是坐标原点，则称E为有界集． (7) 无界集：一个集合如果不是有界集，就称这集合 为无界集．

第一节多元函数的基本概念例如，集合 ((x,)[1<x2+2<2)，是区域、有界集集合 ((x,)[1≤x2+2≤2)，是闭区域、有界集集合(x,)[1<x2+2≤2)，既非开集，也非闭集XxX有界开区域有界闭区域非开非闭，但有界MathGS上页下页返回公式线与面数学家

第一节 多元函数的基本概念 例如， 集合 {( , )|1 2}, 2 2 x y  x + y  是区域、有界集. 集合 {( , )|1 2}, 2 2 x y  x + y  是闭区域、有界集. 集合 {( , )|1 2}, 2 2 x y  x + y  既非开集，也非闭集. 有界开区域 x y O 有界闭区域 x y O 非开非闭，但有界 x y O

第一节多元函数的基本概念*4.n维空间n元有序数组（x,x2，,x）的全体所构成的集合记作Rn,即J Rn=RxRx...xR={(xi,x2,..,xn)| x R, k=1,2,...,n ).Rn中的每一个元素用单个粗体字母x表示，即x=(x,x2,,xn).任给 x=(xi,X2,...,xn), y=(y1,y2,..,yn)eR" , aeR,定义：x+y=(xi+yi,X2+y2,",xn+yn),线性运算ax=(ax, ax2, ..., axn).MathGS下页返回公式线与面数学家上页

第一节 多元函数的基本概念 *4. n 维空间 n 元有序数组 的全体所构成的集合记作 Rn , 即 R = R  R  R n Rn中的每一个元素用单个粗体字母 x 表示, 即 定义: ( , , , ) . 1 2 n  x =  x  x   x ( , , , ) , 1 1 2 2 n n x + y = x + y x + y  x + y 线性运算 任给

第一节多元函数的基本概念其元素称为点定义了线性运算的R称为n维空间或n维向量．x；称为x的第i个坐标或第i个分量特别地，Rn中的零元0称为Rn中的坐标原点或n维零向量.Rn中的两点x=（xi,,xn）,=（yi,,yn）的距离定义为p(x, y)=x-yl= /(xi -y) +..+(x, -yn)?这种距离称为欧氏距离返回MathGS公式上页下页线与面数学家

第一节 多元函数的基本概念 其元素称为点 或n 维向量. xi 称为 x 的第 i 个坐标或第 i 个分量. 定义了线性运算的Rn称为 n 维空间, 特别地，Rn中的零元0称为Rn中的坐标原点或n维零 向量． 定义为 ( , , ) , ( , , ) 1 n 1 n R x = x  x y = y  y n中的两点 的距离 这种距离称为欧氏距离．