《高等数学》课程教学资源（课件讲稿）第二章_2.1导数的概念

导数思想最早由法国第二章数学家Ferma在研究导数与微分极值问题中提出微积分学的创始人英国数学家Newton德国数学家Leibniz导数描述函数变化快慢微分学微分描述函数变化程度都是描述物质运动的工具（从微观上研究函数）

第二章 微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数) 导数与微分 导数思想最早由法国 数学家 Ferma 在研究 极值问题中提出. 英国数学家 Newton

第一节 导数的概念问题的提出二、 导数的定义三、由定义求导数四、导数的几何意义与物理意义五、可导与连续的关系思考题六、小结

第一节 导数的概念 • 一、问题的提出 • 二、导数的定义 • 三、由定义求导数 • 四、导数的几何意义与物理意义 • 五、可导与连续的关系 • 六、小结 思考题

问题的提出一、1.直线运动的瞬时速度问题如图,求t,时刻的瞬时速度,其中位置函数为s,并有s = f(t),某点从时刻t,到时刻t内,运动时间△t,位置从s.=f(t)移到s = f(t),AAsf(t)-f(t)SSo平均速度：Att-tot-to当t→t,时,取极限得f(t)-f(t.)S-So= lim瞬时速度v=limt-to t-tot-→tot-to

一、问题的提出 1.直线运动的瞬时速度问题 0 0 0 0 , , ( ), , , ( ) ( ), t s s f t t t t s f t s f t =  = 如图,求 时刻的瞬时速度 其中位置函数为 并有 某点从时刻 到时刻 内 运动时间 位置 从 = 移到 0 0 0 0 s s s f t f t ( ) ( ) v t t t t t 平均速度 0 当 t t 时,取极限得 0 0 0 0 0 0 ( ) ( ) lim lim t t t t s s f t f t v t t t t 瞬时速度 → → − − = = − − 0 t t t

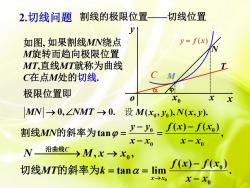
割线的极限位置一一切线位置2.切线问题yy=f(x)如图，如果割线MN绕点M旋转而趋向极限位置MT,直线MT就称为曲线TCMC在点M处的切线aα4极限位置即Xox0xMN -→0,ZNMT →0. i设 M(xo, yo), N(x, y).割线MN的斜率为tan=-=(x)-(x)x-Xox-Xo沿曲线CN>m,x→xo'f(x)- f(xo)切线MT的斜率为k=tanα= limx-→xox-xo

如果割线MN绕点 M旋转而趋向极限位置 MT,直线MT就称为曲线 C在点M处的切线. 极限位置即 MN NMT →  → 0, 0. 设 0 0 M x y N x y ( , ), ( , ). 0 0 0 0 ( ) ( ) tan , y y f x f x MN x x x x  − − = = − − 割线 的斜率为 , , 0 N M x x 沿曲线⎯C→ → 0 0 0 ( ) ( ) tan lim . x x f x f x MT k x x 切线 的斜率为  → − = = − 2.切线问题 割线的极限位置——切线位置  T x0 x  N M o x y y = f (x) C 如图

导数的定义二、定义设函数y=f(x)在点x,的某个邻域内有定义，当自变量x在x.处取得增量△x(点x。+△x仍在该邻域内)时，相应地函数y取得增量Ay= f(x,+Ax)-f(x);如果Ay与△x之比当△x→0时的极限存在，则称函数y=f(x)在点x,处可导，并称这个极限为函数y=f(x)在点x,处的导数，记为y"X=Xo

二、导数的定义 0 0 0 0 0 0 0 0 ( ) , ( ) , ( ) ( ); 0 , ( ) , ( ) , , x x y f x x x x x x x y y f x x f x y x x y f x x y f x x y = =  +   = +  −    → =  设函数 在点 的某个邻域内 有定义 当自变量 在 处取得增量 点 仍在该邻域内 时 相应地函数 取 得增量 如果 与 之比当 时的极限存在 则称函数 在点 处可导 并称这个极限为函 数 在点 处的导数 记为 定义

业df(x)或[x=x, ,或f(x).X=XodxAyf(x + Ax)- f(x,)即limlimV-X=XoArAr>0△AxAr-→0f(xo +h)- f(x)其它形式f'(x,)= limhh-→0f(x)- f(xo)f'(x)= limx-xox-xo

其它形式 0 0 0 ( ) , ( ). x x x x dy df x f x dx dx = = 或 或  即

关于导数的说明：点导数是因变量在点x.处的变化率，它反映了因变量随自变量的变化而变化的快慢程度。★如果函数 = f(x)在开区间I内的每点处都可导，就称函数f(x)在开区间I内可导

. , 0 慢程度 反映了因变量随自变量的变化而变化的快 点导数是因变量在点 x 处的变化率 它 , ( ) . ( ) 处都可导 就称函数 在开区间 内可导 如果函数 内的每点 f x I y = f x I ★ ★ 关于导数的说明：

★对于任一 x E I,都对应着 f(x)的一个确定的导数值.这个函数叫做原来函数f(x)的导函数业df(x)或记作y',f'(x),dxf(x+ △x)- f(x)即 y'= limAxAr→0f(x+h)- f(x)或 f'(x)=limhh-→0注意: 1. f'(x)= f'(x)x=X0

, ( ) . ( ) . ( ) , ( ), . x I f x f x dy df x y f x dx dx    对于任一 都对应着 的一个确定的 导数值 这个函数叫做原来函数 的导函数 记作 或x f x x f x y x  + −  =  → ( ) ( ) lim 0 即 . ( ) ( ) ( ) lim 0 h f x h f x f x h + −  = → 或 注意: 1. ( ) ( ) . 0 0 x x f x f x =  =  ★

例1填空：f(x-Ax)-f(x) = -f(x,)(1)设 f'(x) limAr-0Axf(x)limf'(O)(2) 设f(O)=0,f'(O)存在，则1x-→0x(3)设f(x)为偶函数,f'(O)存在，则 f'(O)= 0(4) f(1) = 0, f(1) = 2, lim nf(1- -) = _-2n8n

例1 填空： _. 0 0 0 Δ 0 ( Δ ) ( ) (1) ( ) lim x Δ f x x f x f x x − − 设 →  = (2) 设 存在，则 . →  = 0 ( ) (0) = 0, (0) lim x f x f f x (3) 设 f x f f ( ) (0) (0 为偶函数，   存在，则 ) = . . →   1 (4) (1) = 0, (1) = 2, lim (1 ) = n f f nf n −

单选题03设置2分设f(x)可导且下列极限存在，则（）成立f(xo -2△x)- f(x)limXA.r->0△x2f(x)- f(0)= f(0)BlimX-0xf(x0 - Ar)- f(o) = f(x0)lim△x△x->0f(a+2h)-f(a)lim=f(a)hh->0提交

设f(x)可导且下列极限存在，则（）成立 A B C D 提交 单选题 2分