《高等数学》课程教学资源（课件讲稿）第七章_7.4一阶线性微分方程

第四节一阶线性微分方程一阶线性微分方程二、 伯劳利方程三、小结

第四节 一阶线性微分方程 • 一、一阶线性微分方程 • 二、伯努利方程 • 三、小结

一、一阶线性方程一阶线性微分方程的标准形式+ P(x)y=Q(x)dx当Q(x)=0，上方程称为齐次的。当Q(x)丰0，上方程称为非齐次的.dxdy例如xsint+t2，线性的；V+x二drdt非线性的.yy-2xy = 3, y'-cos y = 1

( ) ( ) dy P x y Q x dx   一阶线性微分方程的标准形式: 当Q(x)  0, 上方程称为齐次的. 上方程称为非齐次的. 当Q x( ) 0,  例如 , 2 y x dx dy   sin , 2 x t t dt dx   yy  2xy  3, y  cos y  1, 线性的; 非线性的. 一、一阶线性方程

一阶线性微分方程的解法dy+ P(x)y = 0.1.一阶线性齐次方程dxdy变量分离得2 = -P(x)dx,j=-[ P(x)dt,两端积分得1即In / y |=-{P(x)dx + InC1,齐次方程的通解为 J=Ce-[ P(x)te

 P(x) y  0. dx dyP(x)dx, y dy   ( ) ,     P x dx y dy ln | | ( ) ln , C1 y   P x dx   齐次方程的通解为 . ( )    P x dx y Ce 1.一阶线性齐次方程 一阶线性微分方程的解法 变量分离得 两端积分得 即

dy2.一阶线性非齐次方程+ P(x)y = Q(x)dxQ(x) _ P(x) dx,dy讨论1Q(x)dx-[ P(x)dx,两边积分 In|=[yg(x)设dx为v(x), :. In||= v(x)- [ P(x)dx,y即 =e'(x)e-[P(x)dx。非齐次方程通解形式与齐次方程通解相比： C→u(x)

2. 一阶线性非齐次方程 P(x) y Q(x). dx dy   讨论 ( ) , ( ) P x dx y Q x y dy          两边积分 ( ) ln ( ) , Q x y dx P x dx y     ( ), ( )dx v x y Q x 设  为    ln ( ) ( ) , y v x P x dx  . ( )  ( )  v x P x dx 即 y e e 非齐次方程通解形式 与齐次方程通解相比: C u x  ( )

常数变易法把齐次方程通解中的常数变易为待定函数的方法y= u(x)e-Jp(x)de作变换y'=u(x)e- P(r)e-J P(x)dx+ u(x)[-P(x)]e将y和代入原方程得

常数变易法 把齐次方程通解中的常数变易为待定函数的方法. 作变换 ( ) ( ) P x dx y u x e    ( ) ( )[ ( )] , ( ) ( )        P x dx  P x dx y u x e u x P x e 将y和y代入原方程得

d*-P(x)ue-[ p(x)dxu'e-J p(x)dx+ P(x)ue-[ p(x)dx=Q(x)u'(x)e-J P(x)d即x =Q(x),积分得 u(x)=Je(x)el P(x)dcadx +C,一阶线性非齐次微分方程的通解为：*dx + CJe- (r)day=If e(x)el ()at= Ce-J p(x)dxP(x)dx+e (w)a J (x)e/ Pdxte非齐次方程特解对应齐次方程通解

( ) ( ) , ( ) u x Q x e dx C P x dx     ( ) ( ), ( ) u x e Q x P x dx     积分得 一阶线性非齐次微分方程的通解为: ( ) ( ) [ ( ) ] P x dx P x dx y Q x e dx C e       Ce e Q x e dx P x dx P x dx P x dx         ( )  ( ) ( ) ( ) 对应齐次 方程通解 非齐次方程特解 ( )d ( )d ( )d ( ) ( ) ( ) P x x P x x P x x u e P x ue P x ue Q x           即

2ydy(x+1)%例1.解方程dxx+12dxdy2ydy即：0,解：先解dxx+1x+1y积分得In||=2In|x+1|+In|C|,即 y=C(x+1)用常数变易法求特解。令y=u(x)·(x+1)",则y' =u'.(x+1)° +2u·(x+1)代入非齐次方程得 u'=(x+1)"=号(x+1)*+C解得(x+1/%+c故原方程通解为=(x+1)2

例1. 解方程 5 2 d 2 ( 1) . d 1 y y x x x     解: 先解 d 2 0 , d 1 y y x x    即 d 2d 1 y x y x   积分得 ln 2ln 1 ln , y x C    即 2 y C x   ( 1) 用常数变易法求特解. 令 2 y u x x    ( ) ( 1) , 则 2 y u x u x         ( 1) 2 ( 1) 代入非齐次方程得 1 2 u x    ( 1) 解得 3 2 2 ( 1) 3 u x C    故原方程通解为 3 2 2 2 ( 1) ( 1) 3 y x x C          

R例2.有一电路如图所示，其中电源电动势为E=Esinのt,电阻R和电KLE感L都是常量，求电流(t)解：列方程.由回路电压定律：在闭合回路中，所有支路上的电压降为0已知经过电阻R的电压降为Ridi经过 L的电压降为-LdtRE...didisinot因此有E-L即Ri=0,一一十二LLdtdt初始条件：ilr=o=0

例2. 有一电路如图所示, 电动势为 sin , E E t  m  电阻 R 和电 i t( ) . ∼ L E R K 解: 列方程 . 已知经过电阻 R 的电压降为R i 经过 L的电压降为 d d i L t  因此有 d 0 , d i E L R i t    即 d sin d E t m i R i t L L    初始条件: 0 0 t i   由回路电压定律: 其中电源 感 L 都是常量, 求电流 在闭合回路中, 所有支路上的电压降为 0

RdiE....sinotmRi=+LdtLil t=o=0KLAE解方程:利用一阶线性方程解的公式可得sinatelsdEdti(t)= e-J&drmdt+CLE(Rsinot-w Lcosot)+cet.mR"+'L?QLE由初始条件:il==0 得 =_HR?+OL

∼ L E R K 解方程: d sin d E t m i R i t L L    0 0 t i   由初始条件: 0 0 t i   得 2 2 2 LE m C R L     i t( )  d d sin d R R t t L L E m e te t C L             2 2 2 ( sin cos ) R t m L E R t L t C e R L          利用一阶线性方程解的公式可得

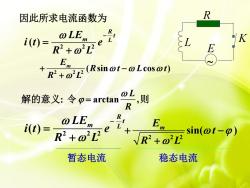
R因此所求电流函数为ROLEKLmLi(t)=1eER'+o"L?Em(Rsinot-o Lcosot)R'+OL?wL则解的意义：令β=arctanRRLEELmi(t)=mesin(@t-Φ)+R?+O'LVR?+0L?暂态电流稳态电流

2 2 2 ( ) R t m L LE i t e R L      2 2 2 ( sin cos ) E m R t L t R L        2 2 2 ( ) R t m L LE i t e R L      2 2 2 sin( ) E m t R L       暂态电流 稳态电流 arctan , L R  令  则 ∼ L E R K 因此所求电流函数为 解的意义: