《高等数学》课程教学资源（课件讲稿）第三章_3.1中值定理

第三章微分中值定理与导数的应用罗尔中值定理推广泰勒公式↓拉格朗日中值定理中值定理（第三节）柯西中值定理研究函数性质及曲线性态应用利用导数解决实际问题

第三章 中值定理 应用 研究函数性质及曲线性态 利用导数解决实际问题 罗尔中值定理 拉格朗日中值定理 柯西中值定理 泰勒公式 (第三节) 推广 微分中值定理 与导数的应用

中值定理(mean value theorem变点指导数在某个区间内所具有的一一些重要性质,它们都与自变量区间内部的某个中生态，间值有关要用导数来研究函数的全部性态，还需架起新的“桥梁

2 因为导数是函数随自变量变化的瞬时变 所以可借助导数来研究函数. 但每一点 的导数仅仅是与局部有关的一点的变化性态, 要用导数来研究函数的全部性态,还需架起新 的“桥梁”. 中值定理(mean value theorem) 化率, 指导数在某个区间内所具有的一些重 要性质,它们都与自变量区间内部的某个中 间值有关

第一节中值定理、罗尔中值定理T二、拉格朗日中值定理三、柯西中值定理四、小结

第一节 中值定理 • 一、罗尔中值定理 • 二、拉格朗日中值定理 • 三、柯西中值定理 • 四、小结

一、费马引理费马Pierre de Fermat1601～1665法国著名数学家，被誉为“业余数学家之王

费 马 Pierre de Fermat 1601～1665 法国著名数学家， 被誉为“业余数学 家之王” 一、费马引理

费马生性内向，谦抑好静．他通晓法语、意大利语、西班牙语、拉丁语和希腊语.语言方面的博学给费马的数学研究提供了语言工具和便利，使他有能力学习和了解阿拉伯和意大利的代数以及古希腊的数学.费马一生从未受过专门的数学教育然而，在17世纪的法国还找不到哪位数学家可以与之匹敌.他是解析几何的发明者之一；对于微积分诞生的贡献仅次于牛顿、莱布尼茨；他是概率论的主要创始人，他是独承17世纪数论天地的人：此外费马对物理学也有重要贡献.一代数学大才费马堪称是17世纪法国最伟大的数学家：

费马生性内向, 谦抑好静. 他通晓法语、意大 利语、西班牙语、拉丁语和希腊语. 语言方面的 博学给费马的数学研究提供了语言工具和便利, 使 他有能力学习和了解阿拉伯和意大利的代数以及 古希腊的数学. 费马一生从未受过专门的数学教育, 然而, 在17世纪的法国还找不到哪位数学家可以与 之匹敌. 他是解析几何的发明者之一；对于微积分 诞生的贡献仅次于牛顿、莱布尼茨;他是概率论的 主要创始人, 他是独承17世纪数论天地的人. 此外, 费马对物理学也有重要贡献. 一代数学大才费马堪 称是17世纪法国最伟大的数学家

费马引理设函数f(x)在点x.的某邻域U(x)内有定义，并且在x.处可导，如果对任意xU(x)的，有f(x)≤ f(x.)(或f(x) ≥ f(x)那么f'(x)= 0

0 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( )( ( ) ( )) ( ) . f x x U x x x U x f x f x f x f x f x     = 设函数 在点 的某邻域 内有定义，并且在 处可导，如 果对任意 的，有 费 那么 理 或 马引

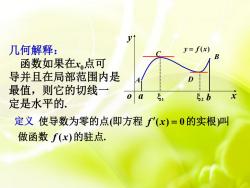
V几何解释：y= f(x)B函数如果在x.点可导并且在局部范围内是DA最值，则它的切线一x5,0E2ba定是水平的定义 使导数为零的点(即方程 f'(x)=0的实根)叫做函数f(x)的驻点

o a 1  2 b x y y = f (x) A B C D 几何解释： 函数如果在x0点可 导并且在局部范围内是 最值，则它的切线一 定是水平的. ( ) . ( ( ) 0 ) 做函数 的驻点 使导数为零的点 即方程 的实根 叫 f x 定义 f  x =

证： 不妨设Vx+△x EU(x),f(x。+△x)≤ f(xo),f(xo +Ax) - f(xo)≤0;若△r>0，则有Axf(x。 +Ax)- f(x)≤0;:. f'(x)= limAx△r->+0f(xo + △x)- f(xo)若△x<0，则有≥0;Axf(xo +Ax)- f(x)≥0;.:. f'(x) = limAxAr→-0又：f(x)存在,. f'(x) =f(x):: 只有 f'(x。)= 0.证毕

证: 0 0 0 0 不妨设 +   +   x x U x f x x f x ( ), ( ) ( ), 证毕 若 x  0, 0 0 0 ( ) ( ) ; f x x f x x 则有 +  −   若 x  0, 0 0 0 ( ) ( ) ; f x x f x x 则有 +  −   0 0 0 0 0 ( ) ( ) ( ) lim ; x f x x f x f x x −  →− +  −  =    0 0 0 0 0 ( ) ( ) ( ) lim ; x f x x f x f x x +  →+ +  −  =    0 又 f x ( ) , 存在 0 0 f x f x ( ) ( ). − +  =   0  = 只有 f x ( ) . 0

导数教零点定理定理：设（x）在[a.b]上可导，且f（a)(b）0，(x）在[a,6上的最小值为m，m=f（），由f()-(a)20及极限的保号性得，在x-a的某个右邻城内，f'(a)=lim$x-af(x)-f(a)a),于是(+)0及极限的保号性得，在×=6的菜个左邻城内，同理，由f（0）=limm142x-b()-J(6)>0x<b)，于是(0)<J)，7-6综上得，5+a,b，因此，5e（a,b)，由费马引理得，（)=0注：费马引理：若（x）在处可导，在的某够城内均有了（）≤（）（或（x)2（）），1(元）=0

导级零点定理的几何意义f(a)F(o)0，或者J(a)>0.J(b)0,则在a的右够域内（）0.J(b)/(@)，在b的左邻域内()>/(b)，此时，J（x）的最大值M必然在（a，b）内的某点处取得，曲线y=（x）在处的切线平行于出国留学网×轴，即厂（）=0、反映在图像上即下面的图1和图2WWWLIITUEBE.COM-Oob11图2