《高等数学》课程教学资源（课件讲稿）第一章_1.1映射与函数

高等数学刘宣江

高等数学 刘宣江

高等数学学习各门理工专业的重要基础解决各种专业问题的重要工具培养分析能力，锻炼理性思维提高综合素质，享受数学之美重要

高等数学 学习各门理工专业的重要基础 解决各种专业问题的重要工具 培养分析能力，锻炼理性思维 提高综合素质，享受数学之美 重要

2！7.2如何学好高等数学数学思维方法的领会，分析问题能力的加强，解题水平的提高，仅依靠阅读教材是远远不够的。好的辅助工具会给大家提供及时的帮助！

数学思维方法的领会，分析问题能力 的加强，解题水平的提高，仅依靠阅读教 材是远远不够的。好的辅助工具会给大家 提供及时的帮助！

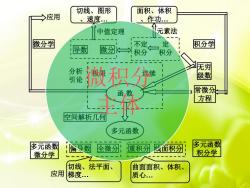
切线、图形面积、体积一>应用作功...、速度价元素法中值定理微分学不定定积分学导数微分积分积分无穷分析微积分级数引论常微分函数方程主体空间解析几何多元函数多元函数多元函数线面积分全微分偏导数重积分积分学微分学切线、法平面、曲面面积、体积、应用梯度...质心

导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 空间解析几何 无穷 级数 常微分 方程 切线、法平面、 梯度. 曲面面积、体积、 质心. 微积分 主体

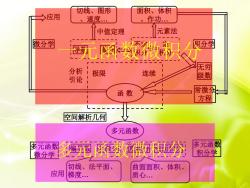
切线、图形面积、体积应用作功、速度，元素法中值定理微分学积分学海国数微积分无穷分析极限连续级数引论常微分函数方程空间解析几何多元函数多元函数图元函数多编儿承数微务积分学微分学切线、法平面曲面面积、体积、应用梯度...质心

导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 空间解析几何 无穷 级数 常微分 方程 切线、法平面、 梯度. 曲面面积、体积、 质心. 一元函数微积分 多元函数微积分

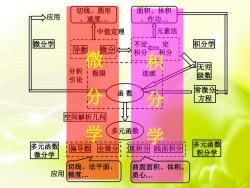
切线、图形面积、体积一>应用、速度.作功元素法中值定理微分学不定定积分学厚数微分K积分积分微禾积无穷分析极限连续级数引论常微分分函数分学方程空间解析几何R7学多元函数多元函数多元函数偏导数全微分重积分线面积分积分学微分学切线、法平面、曲面面积、体积应用梯度...质心

导数 微分 函 数 分析 极限 连续 引论 微分学 不定 积分 定 积分 积分学 应用 中值定理 元素法 切线、图形 、速度. 面积、体积 、作功. 多元函数 多元函数 偏导数 全微分 重积分 线面积分 微分学 多元函数 积分学 应用 空间解析几何 无穷 级数 常微分 方程 微 分 学 积 分 学 切线、法平面、 梯度. 曲面面积、体积、 质心

第一章函数与极限函数一研究对象分析基础 极限 一研究方法连续一研究桥楽

第一章 分析基础 函数 极限 连续 — 研究对象 — 研究方法 — 研究桥梁 函数与极限

第一节映射与函数一、集合二、 映射三、 函数

第一节 映射与函数 一、集合 二、映射 三、函数

一、映射1. 映射设X、Y是两个非空集合，如果存在一个法则f，使得对于X中每个元素x，按法则f在Y中有唯一确定的元素y与之对应，则f称为从X到Y的映射记作f:X-→Y其中y称为元素x（在映射f下）的像，并记作f(x)，即y= f(x)而元素x称为元素y（在映射f下）的一个原像；集合X称为映射f的定义域，记作D，即D，=X；X中所有元素的像所组成的集合称为映射f的值域，记作R,或f(X)，即R, =f(X)=(f(x)IxEX)

一、映射 1. 映射 设 是两个非空集合，如果存在一个法则 ,使得对于 中每个元素 ，按法则 在 中有唯 一确定的元素 与之对应，则 称为从 到 的映射， 记作 其中 称为元素 （在映射 下）的像，并记作 ， 即 而元素 称为元素 （在映射 下）的一个原像；集 合 称为映射 的定义域，记作 ，即 ； 中所有元素的像所组成的集合称为映射 的值域， 记作 或 ，即 X、Y f X x f Y y f X Y f : X  Y y x f f ( x) y  f ( x) x y f X f Df Df  X X f Rf f (X ) R f (X ) { f ( x) | x X } f   

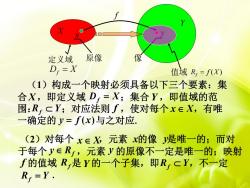
X1原像像定义域D, = X值域R,=f(X)（1）构成一个映射必须具备以下三个要素：集合X，即定义域D，=X：集合Y，即值域的范围:R,，CY；对应法则f，使对每个xEX，有唯一确定的 =f(x)与之对应（2）对每个xeX元素 x的像堤唯一的：而对于每个ERf，元素的原像不一定是唯一的；映射f的值域R,是Y的一个子集，即R，CY，不一定R, =Y

X Y x y f 定义域 原像 像 D X f  值域 ( ) R f X f  （1）构成一个映射必须具备以下三个要素：集 合 ，即定义域 ；集合 ，即值域的范 围： ；对应法则 ，使对每个 ，有唯 一确定的 与之对应. X Df  X Y Rf  Y f x  X y  f ( x) （2）对每个 ，元素 的像 是唯一的；而对 于每个 ，元素 的原像不一定是唯一的；映射 的值域 是 的一个子集，即 ，不一定 . x  X x y Rf y  y f Rf Y Rf  Y Rf  Y