《高等数学》课程教学资源（课件讲稿）第七章_7.5可降阶的高阶微分方程

第五节可降阶的高阶微分方程、J(n) = f(x) 型的微分方程二、J"=f(x,y)型的微分方程三、J"=f(y,J)型的微分方程

第五节 可降阶的高阶微分方程 • 一、 型的微分方程 • 二、 型的微分方程 • 三、 型的微分方程 ( ) ( ) y f x n  y f x y    ( , ) y f y y    ( , )

一、J(n)=f(x)型的微分方程dz令z= y(n-1), 则=(")=(x),因此z=J f(x)dx+C)即y(n-1) = [ f(x) dx + C,y(n-2) = Jf f(x)dx+C,ldx+C,同理可得= JJ f(x)dx)dx+C, dx+C,依次通过n次积分，可得含n个任意常数的通解

令 ( 1) , n z y   d ( ) ( ) , d n z y f x x 则   因此 1 z f x x C   ( )d  即 ( 1) 1 ( )d n y f x x C     同理可得 ( 2) 1 2 [ ( )d ]d n y f x x C x C       依次通过 n 次积分, 可得含 n 个任意常数的通解 . 1 2    [ ( )d ]d d f x x x C x C   一 、y f x ( ) n  ( )型的微分方程

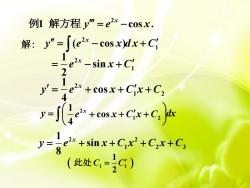
例1 解方程 y"=e2x-cos x.(e2x - cos x)dx+C)解：J"=2x- sin x + Cie121-2x+ cos x+C'x+C,e14-2x+ cos x+Cix+C, Jix4-2x+ sin x+C,x+C,x+CV=8(此处Cci)

解: 2 1 ( cos ) x y e x d x C       2 1 1 sin 2 x    e x C 2 1 2 1 cos 4 x y e x C x C       2 2 1 2 3 1 sin 8 x y e x C x C x C      2 1 2 1 cos 4 x y dx e x C x C             2 1 cos . x 例 解方程 y e x      1 1 1 2 此处 C C  

例2质量为m的质点受力F的作用沿0x轴作直线运动.设力F仅是时间t的函数：F=F(t).在开始时刻t =0 时 F(O)= F,随着时间t 的增大,此力 F 均匀地减小,直到t=T时，F(T)=0.如果开始时质点位于原点,且初速度为零,求质点在0<t≤T时的运动规律。IF解 设x= x(t)表示在时刻 t 时质点的位置F:FFo(1根据牛顿第二定律，质点运动的微分方程为d'xF(t)mOdt?T t由题设t=0时，F(O)=F，且力随着时间的增大而均匀地减小；所以F(t)= F - kt;

解 设x  x(t ) 表示在时刻 t 时质点的位置, 根据牛顿第二定律,质点运动的微分方程为 F（t） dt d x m  2 2 0 由题设t F F   0 (0) 时， ，且力随着时间的增大而均匀 地减小；所以 0 F t F kt ( ) ;   例2 质量为 的质点受力 的作用沿 轴作直线 运动.设力 仅是时间 的函数: .在开始时 刻 时 ,随着时间 的增大,此力 均 匀地减小,直到 时, .如果开始时质点 位于原点,且初速度为零,求质点在 时 的运 动规律. F  F(t) m F Ox F t t  0 0 F(0)  F t F t  T F(T)  0 0  t  T t F o F  (1 ) 0 T t F  T F0

又当t = T时,F(T)=0， 从而1FF(t)= F(1-)F=FoFo(1-d'xTF方程为X(1dt?m0Tt-初始条件为0x /t==02Fdx两端积分得(t+Cdt2Tm一m代入初始条件lt=0= 0得C=0

又当t  T时,F(T)  0, 从而 ( ) (1 ) 0 T t F t  F  方程为 (1 ) 0 2 2 T t m F dt d x   初始条件为 | 0, | 0 t0 t0 dt dx x 两端积分得 1 2 0 ) 2 ( C T t t m F dt dx    代入初始条件 | 0 0 0 C1 dt dx t 得 t F o F  (1 ) 0 T t F  T F0

Fdx0于是方程变为一m(t2TmFo-L)再积分一次得)+Cx=6Tm将条件xl=0=代入上式,得C, = 0于是,所求质点的运动规律为H0≤t≤TX=6Tm

于是方程变为 ) 2 ( 2 0 T t t m F dt dx   再积分一次得 2 2 3 0 ) 2 6 ( C T t t m F x    将条件 x | t0 0 代入上式,得 0 C2  于是,所求质点的运动规律为 t T T t t m F x   ) 0  2 6 ( 2 3 0

二、y"=f(x,y')型的微分方程解法：令y'= p，则y"= p,故有p'= f(x,p)此时，该二阶微分方程变为一阶微分方程，求出一阶微分方程的通解后再两边积分即可

解法： 令y p   , 则y p    , 故有p f x p   ( , ) 此时，该二阶微分方程变为一阶微分方程，求出 一阶微分方程的通解后再两边积分即可 二、y f x y    ( , )型的微分方程

设其通解为 p=@(x,C)y'= Φ(x,Cl)则得再一次积分，得原方程的通解y=[p(x,C)dx+C

设其通解为 1 p x C   ( , ) 则得 1 y x C    ( , ) 再一次积分, 得原方程的通解 1 2 y x C x C    ( , )d 

例3求微分方程(1+ x)y" = 2xy满足初始条件y lx=0= 1, y' Ix=0= 3的特解.解：设y=p,代入方程并分离变量得2xdp_dx21+xp两边积分得到 In|pl= In(1+x2)+C即 p=J'=C(1+x’)(C,=±eC)两边再积分得y=C(x+=)+C,3

2 0 0 3 (1 ) 2 | 1, | 3 x x x y xy y y         例 求微分方程 满足初始条件 的特解. 解： 设 y p   , 代入方程并分离变量得 dx x x p dp 2 1 2   两边积分得到 2 ln ln(1 ) p x C    2 1 1 (1 ) ( ) C 即 p y C x C e       两边再积分得 3 1 2 ( ) 3 x y C x C   

由条件ylx=o=3,得C,=3又由条件l=0=1,得C,=1于是所求方程的特解为：y = x3 + 3x + 1

0 2 | 1, 1 x 又由条件 y C    得 于是所求方程的特解为： 3 1 3 y  x  x  0 1 | 3, 3 x y C  由条件    得