《高等数学》课程教学资源（课件讲稿）第3章 第2讲 洛必达法则

高等数学（上册）第3章微分中值定理与导数的应用第2讲洛必达法则人民邮电出版社POSTS&TELECOMPRESS

高等数学（上册） 第2讲 洛必达法则 第3章 微分中值定理与导数的应用

R人邮教育本讲内容w.yjinaoyu.cc0关型01未定式型未定式和“L002其他类型的未定式0准，0°，￥-￥，1￥，￥0

01 02 其他类型的未定式 “ ”型未定式和“ ”型未定式 本 讲 内 容

2”型未定式01”型未定式和COAORA人邮教育O定理3.4洛必达法则口设f(x）、g(x)在xo的某去心邻域内有定义，若lim f(x)=0 lim g(x)=0(1XRXo,xRXo(2f(x)、g(x）在x的某去心邻域内可导，且gdx)20;)dx)lim(3存在（或无穷大），@xogdx))f(x)fdx)limI lim则g(x)XRxo gdx)XRXO

01 “ ”型未定式和“ ”型未定式 定理 3.4 洛必达法则ᵮ 设 、 在 x0 的某去心邻域内有定义，若 （1 ） ， ； （2 ） 、 在x0的某去心邻域内可导，且 ； （3 ） 存在（或无穷大）， 则 . 3

01”型未定式和”型未定式COAOR人邮教育O洛必达法则工定理3.5设f(x）、g(x）在x的某去心邻域内有定义，若lim f(x)=￥ lim g(x)=￥(1XRX0rRXof(x）、g(x）在x,的某去心邻域内可导，且gdx)！0;2Idx)lim(3存在（或无穷大），gdx)XRXOf(x)lim Jdx)lim则XRX0g(x)xXogdx)

定理 3.5 洛必达法则Ⅱ 设 、 在 x0 的某去心邻域内有定义，若 （1 ） ， ； （2 ） 、 在x0的某去心邻域内可导，且 ； （3 ） 存在（或无穷大）， 则 . 01 “ ”型未定式和“ ”型未定式 4

0”型未定式01型未定式和“0000RA人邮教育0sinax求极限lim例（a,b为常数，且b10）1r@0 sin bx0D解该极限为型不定式，由洛必达法则，得000sin axacosaxalimlimbx@0 sinbxxaobcosbx

例 1 5 解 该极限为“ ” 型不定式，由洛必达法则，得 5 01 “ ”型未定式和“ ”型未定式 求极限 （a, b 为常数，且 ）

0”型未定式01型未定式和“COA0RA人邮教育0x- sinx艮lim求极限例2x?00O解该极限为型不定式，由洛必达法则，得0001- cosxsinxX-limlimx33x2XROXRO00sinx=lim6xXR016

例 2 6 解 该极限为“ ” 型不定式，由洛必达法则，得 6 01 “ ”型未定式和“ ”型未定式 求极限

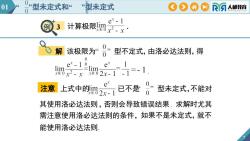
型未定式01型未定式和COARA人邮教育O计算极限lim例3rROx0D解该极限为型不定式，由洛必达法则，得00er1Cerlimlim-1-12x- 1ROx?0-Xer0注意已不是上式中的im型未定式，不能对0x@02x-1其使用洛必达法则，否则会导致错误结果：求解时尤其需注意使用洛必达法则的条件，如果不是未定式，就不能使用洛必达法则

例 3 7 计算极限 ． 该极限为“ ” 型不定式，由洛必达法则，得 上式中的 已不是“ ” 型未定式，不能对 其使用洛必达法则，否则会导致错误结果. 求解时尤其 需注意使用洛必达法则的条件，如果不是未定式， 能使用洛必达法则. 注意 就不 解 . 7 01 “ ”型未定式和“ ”型未定式

”型未定式01型未定式和O0A0R人邮教育0x3 - 12x+16计算极限lim例x2x3.2x2-4x+80o解该极限属于型未定式，由洛必达法则，得000x3 - 12x+1603x2- 12306xlimlimlim2x@2x3- 2x2- 4x+8x@23x2-4x-46x- 4xR2本例中使用了两次洛必达法则

8 计算极限 ． 该极限属于“ ” 型未定式，由洛必达法则，得 本例中使用了两次洛必达法则. 例 4 8 解 . 01 “ ”型未定式和“ ”型未定式

型未定式01型未定式和“CO0RA人邮教育0tanx- x计算极限lim例5x@ox?sinx.0这是“型未定式，先对分母中的乘积因子O解0sinx利用等价无穷小x(x0)进行代换，再由洛必达法则，得0sec2x- 10tanx-tanx- x=lim= limlim3x2XXROXROXROxsinxtan? x11tanx= limlim3x23X?03xR0x

9 计算极限 ． 这是“ ” 型未定式，先对分母中的乘积因子 利用等价无穷小 ( )进行代换， 再由洛必达法则，得 例 5 9 解 . 01 “ ”型未定式和“ ”型未定式

06601”型未定式型未定式和“COAR人邮教育0Inxlim(ni N)计算极限例6XR+YO解1?￥Inxxlimlimlim0nr")XR+YXR+YXR+Ynx

10 例 6 计算极限 解 01 “ ”型未定式和“ ”型未定式