《高等数学》课程教学资源（课件讲稿）第3章 第6讲 弧微分与曲率

高等数学（上册）第3章微分中值定理与导数的应用第6讲弧微分与曲率人民邮电出版社POSTS&TELECOMPRESS

高等数学（上册） 第6讲 弧微分与曲率 第3章 微分中值定理与导数的应用

R人邮教育本讲内容nw.ryjinoyu.c弧微分01曲率0203曲率半径与曲率圆

01 弧微分 02 曲率 03 曲率半径与曲率圆 本 讲 内 容

01弧微分COA0R人邮教育曲线y=f(x)上的弧值函数s=s(x)定义设y=f(x) 在(a,b)内有连续导y=f(x)数，M,(xo,yo)作为度量弧长的基点MMo规定：x增大的方向为正向O+x

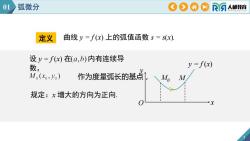
定义 3 曲线 y = f (x) 上的弧值函数 s = s(x). 设 y = f (x) 在 内有连续导 数，                      作为度量弧长的基点， 规定：x 增大的方向为正向. y O x y = f (x) M0 M 01 弧微分

01弧微分OO60R人邮教育对曲线上任意一点M(x，y)，规定有向弧段M,M的值s：①s的绝对值为弧段的长度：②当方向与曲线的正向一致时，s>0显然，s是x③当方向与曲线的正向相反时，S<0，的函数s=s(x)，且单调增加y=fyM (x)Mox

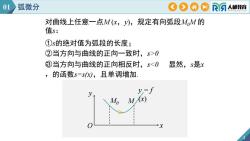
4 对曲线上任意一点M (x，y)，规定有向弧段M0M 的 值s： ①s的绝对值为弧段的长度； ②当方向与曲线的正向一致时，s>0 ；③当方向与曲线的正向相反时，s<0 ， 显然，s是x 的函数s=s(x)，且单调增加. y O x y = f M M (x) 0 01 弧微分

01弧微分COA0人邮教育RADsdslimds = sdx)dx先求s=s(x)的导数弧微分公式ds=？dxDr0DxDs=2Dx在x处给自变量x一增量DxMef (x)tVMo相应的有向弧段的值s有增量MDsxDs= s(x+Dx)- s(x)--0Xox- x+Dx x=M.M&- M.M=MMeDsDsMMdMMdIMMDxDxDxMMDxDs与Dx总是同号的

5 先求s=s(x)的导数 在x处给自变量x一增量 ， 与 总是同号的 相应的有向弧段的值s有增量 ， 弧微分公式 01 弧微分

01弧微分O000RA人邮教育DsMMdMMdDsDrMMdDxDrMetV(Dx) + (Dy)MM 4MoMMMd(Dx)XDsds--1--limdxDrR0Dx0xox-x+Dx xU2MMaDy:U=limX&Dx 0QDx ? 0时,M MDrRoelMMueMM$= /1+(ve)limMMMeRMds = yi+ yedxDylimye弧微分公式DxR 0 Dx或ds= /(dx) +(dy)

弧微分公式 6 时， ， ， 01 弧微分

R人邮教育本讲内容nw.ryjinoyu.c弧微分01曲率0203曲率半径与曲率圆

01 弧微分 02 曲率 03 曲率半径与曲率圆 本 讲 内 容

02曲率COA0人邮教育R1.定义描述：曲线的弯曲程度MMMM,NVMM,M, >N,N,MM, =M,Mj1=j2=jii<j2

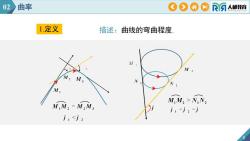
描述：曲线的弯曲程度. 8 1.定义 02 曲率

02曲率COA0RA人邮教育曲线的弯曲程度与下列两个量有关：yM（1）切线转过的角度；（2）弧段的长度MMo+Da(a0x曲率：单位弧长上切线所转过的角度设MM的长度为Ds，切线转过的角度为Dal

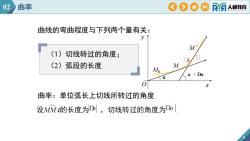
曲线的弯曲程度与下列两个量有关： （1）切线转过的角度； （2）弧段的长度. 曲率：单位弧长上切线所转过的角度. 9 O x y M' M0 M 02 曲率

02曲率COARA人邮教育一平均曲率：品DaV-MM的平均弯曲程度[DsMDaLKMMoDs+ Da1a曲线在点M处的曲率：0xDaK = lim平均曲率的极限DrR ODsdaDa存在，则K若limK=?dsDRODs

平均曲率的极限 平均曲率： 10 的平均弯曲程度 若 存在，则 O x y M' M0 M 02 曲率 曲线在点M处的曲率：