《高等数学》课程教学资源（课件讲稿）第1章——第2节极限的概念与性质

第一章第二节极限的概念与性质一、数列极限二、函数极限HIGHEDUCATION PRESS机动目录上页下页返回结束

第一章 二 、函数极限 一、数列极限 第二节 机动 目录 上页 下页 返回 结束 极限的概念与性质

数列极限的概念一、1、引例一尺之锤，日取其半，万世不竭《庄子*天下篇》HIGHEDUCATION PRESS机动目录上页下页返回结束

一、数列极限的概念 1、引例 一尺之锤， 日取其半， 万世不竭。 -—《庄子*天下篇》 机动 目录 上页 下页 返回 结束

2、定义若数列1 xn及常数α有下列关系总有Vε>0,3正整数N,当n>N时,Xn-aN)即xn U(α,ε)几何解释(n>N)a Xn+2α- X+1α+εHIGHEDUCATIONPRESS机动目录上页下页返回结束

2、定义:若数列 及常数 a 有下列关系 : 当 n > N 时, 总有 记作 此时也称数列收敛 , 否则称数列发散 . 几何解释 : a −  a +  ( ) a −   x  a +  n ( n  N ) 即 x ( a ,  ) n   ( n  N ) x a n n = → lim 或 x → a (n → ) n N +1 x N +2 x 则称该数列 的极限为 a , 机动 目录 上页 下页 返回 结束

n例如，n+ln(n → 8)n+ln+(-1)n-1收敛nn+(-1)n-1→(n n2,4.8.....2hXn =2n → 0(n→8)发散1, -1,1, .,(-1)n+1Xn =(-1)n+1趋势不定HIGH EDUCATION PRESS机动目录上页下页返回结束

例如,  , 1 , , 4 3 , 3 2 , 2 1 n + n +1 = n n xn → 1 (n → ) n n x n n 1 ( 1) − + − = → 1 (n → ) 2 , 4 , 8 ,  , 2 n ,  n n x = 2 →  (n → ) 1 ( 1) + = − n n x 趋势不定 收 敛 发 散 机动 目录 上页 下页 返回 结束

n+(-1)证明数列(x，}的极限为1.例1.已知Xnnn+(-1)证：Xn -1nn二0,欲使xn-15V因此，取 N=[-],则当 n>N 时,就有n+(-1)n<8nn+(-1)故lim xn = limnn→80n→0HIGH EDUCATION PRESS机动目录上页下页返回结束

例1. 已知 证明数列 的极限为1. 证: xn −1 = 1 ( 1) − + − n n n   0 , 欲使 即 只要  1 n  因此 , 取 ], 1 [  N = 则当 n  N 时, 就有 −   + − 1 ( 1) n n n 故 1 ( 1) lim lim = + − = → → n n x n n n n 机动 目录 上页 下页 返回 结束

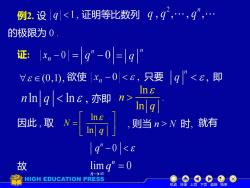
q,q',..,q",..例2.设9In|q lIng就有因此,取N=则当n>N 时,In| q|1q"-0|<故limq" = 0nHIGH EDUCATION PRESS机动目录上页下页返回结束

例2. 设 q  1 , 证明等比数列 证: − 0 n x 欲使 只要 即 亦即 因此 , 取 ln ln N q    =     , 则当 n > N 时, 就有 0 n q −   故 lim 0 n n q → = ln . ln n q   的极限为 0 . 机动 目录 上页 下页 返回 结束

b-ab-a二、收敛数列的性质中a+b1.收敛数列的极限唯一ab2假设lim x,=α及 lim xn =b,且 α00取 ε= b=~, 因lim xn=α,故存在Ni，使当 n>N,时n→8，从而N,时,有n->8[-b取 N= max[Ni,N2 ,则当 n>N时，x,满足的不等式矛盾故假设不真！因此收敛数列的极限必唯一HIGHEDUCATION PRESS机动目录上页下页返回结束

 − 2 3a b 2 2 b a n b a x a − − −  −  二、收敛数列的性质 证: 用反证法. 及 且 a  b. 取 因 lim x a, n n = → 故存在 N1 , 从而 2 a b n x +  同理, 因 lim x b, n n = → 故存在 N2 , 使当 n > N2 时, 有 2 a b n x +  1. 收敛数列的极限唯一. 使当 n > N1 时, 假设 2 2 b a n b a x b − − −  −  n a b  x + 2 2 3b−a  从而 2 a b n x +  矛盾. 因此收敛数列的极限必唯一. max , , 则当 n > N 时, 取 N = N1 N2 故假设不真 ! n x 满足的不等式 机动 目录 上页 下页 返回 结束

2.收敛数列一定有界证：设lim xn=α,取ε=1,则N,当n>N 时,有n-80xn-α<1,从而有[Xn|=[(xn -a)+a|≤|xn-a|+[a<1+|a取M =max(| xi| , [x2], ..., | x~| , 1+a|则有xn≤M (n=1,2,.)由此证明收敛数列必有界此性质反过来不一定成立．例如说明：(-1)n+1数列虽有界但不收敛HIGH EDUCATION PRESS机动目录上页下页返回结束

2. 收敛数列一定有界. 证: 设 取  =1, 则 N , 当 n  N 时, 从而有 x a a  n − +  1+ a 取 M = max x1 , x2 ,  , xN , 1+ a  则有 x  M ( n = 1 , 2 ,  ) . n 由此证明收敛数列必有界. 说明: 此性质反过来不一定成立 . 例如,  1 ( 1 ) + − n 虽有界但不收敛 . x − a  1, n 有 数列 机动 目录 上页 下页 返回 结束

3.收敛数列的保序性limxn=b,且 a>b若 lim xn=an8n→8则NN+,当n>N时,有 x,>ynXn ≥0(≤0) 且 lim xn =a,1.若数列从某项起n0则aα≥0(≤0)2.若lim xn=a,且 a>0(N时,有xn>0(<O)HIGH EDUCATION PRESS机动目录上页下页返回结束

3. 收敛数列的保序性. 2.若 且 时, 有 ( 0), ( 0). 1.若数列从某项起 ( 0) ( 0). 机动 目录 上页 下页 返回 结束 若 且 a b  . 时, 有

4.收敛数列的任一子数列收敛于同一极限证：设数列(xnk}是数列(xn）的任一子数列若 lim xn=a,则ε>O,3N,当n>N时,有n>0[Xn-a|K 时,有XNnknk>nk≥N*********************Nnk从而有<ε,由此证明lim x nkxnkCk-→8HIGH EDUCATION PRESS机动目录上页下页返回结束

********************* x − a   , k n 4. 收敛数列的任一子数列收敛于同一极限 . 证: 设数列 是数列 的任一子数列 . 若 则   0, N , 当 时, 有 现取正整数 K , 使 于是当 k  K 时, 有 nk   N 从而有 由此证明 lim x a . k n k = → ********************* N N x 机动 目录 上页 下页 返回 结束