《高等数学》课程教学资源（课件讲稿）第3章 第4讲 函数的单调性、极值和最值

高等数学（上册）第3章微分中值定理与导数的应用第4节函数的单调性、极值和最值人民邮电出版社POSIS&TELECOMPRESS

高等数学（上册） 第4节 函数的单调性、极值和最值 第3章 微分中值定理与导数的应用

R人邮教育本讲内容w.nyjiaoyu.co01函数的单调性02函数的极值03函数的最值

01 函数的单调性 02 函数的极值 03 函数的最值 本 讲 内 容

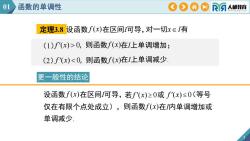
01函数的单调性COAORA人邮教育定理3.8设函数f(x)在区间/可导，对一切xEI有(1)f(x)>0，则函数f(x)在I上单调增加;(2)f(x)<0，则函数f(x)在I上单调减少更一般性的结论设函数f(x)在区间/可导，若f(x)≥0或f(x)≤0（等号仅在有限个点处成立），则函数f(x在内单调增加或单调减少

更一般性的结论 3 定理3.8 （1）f (x)  0，则函数f (x)在I上单调增加； （2）f (x)  0，则函数f (x)在I上单调减少. 设函数 f (x)在区间I可导，若f (x)  0或 f (x)  0（等号 设函数 f (x)在区间I可导，对一切xI有 仅在有限个点处成立）， 单调减少. 则函数f (x)在I内单调增加或 01 函数的单调性

01函数的单调性COR人邮教育讨论单调性的步骤(1)确定y=f(x)的定义域;(2)求f(x)，并求出f(x)单调区间所有可能的分界点（包括f(x)=0、导数不存在的点）并根据分界点把定义域分成相应的区间(3)判断一阶导数f(x）在各区间内的符号从而判断函数在各区间中的单调性

讨论单调性的步骤： 4 （1）确定y  f (x) 的定义域； （2）求f (x), 并求出f (x)单调区间所有可能的分界点 （包括 f (x)  0 、导数不存在的点) 并根据分界点把定义域分成相应的区间; 函数在各区间中的单调性. （3）判断一阶导数f (x)在各区间内的符号从而判断 01 函数的单调性

01函数的单调性COORA人邮教育例讨论函数f(x）=2x3-9x2+12x-3的单调区间，o解（1）函数定义域为（-0,+8)（2）求导数并确定函数的驻点和导数不存在的点：f(x)= 6x2 -18x+12 = 6(x-1)(x-2),由f(x)=0得驻点x,=1,x2=2，该函数没有导数不存在的点（3）根据找到的点划分区间，列表讨论x(-00, 1)(1, 2)(2, +0)12+0f'(x)+0一f(x)单增单减>单增^函数的单调增加区间为(-00,1)、(2,+0),单调减少区间为[1,2]由表可知

5 （1）函数定义域为(,) （2）求导数并确定函数的驻点和导数不存在的点： 2 f (x)  6x 18x12  6(x1)(x 2), f (x)  0 1 2 由 得驻点x 1, x  2 , 该函数没有导数不存在的点． 3 2 例 1 讨论函数f (x)  2x 9x 12x 3的单调区间． 解 01 函数的单调性 （3）根据找到的点划分区间，列表讨论 由表可知, 函数的单调增加区间为(,1)、(2,),单调减少区间为 [1,2]

01函数的单调性CO0RA人邮教育1例2判断函数f(x)=3/x的单调性（1）定义域为(-00,+)解-21x(2) 。f(x)=/在点x=0处导数不存在f'(x):3点x=0把定义域分成两部分区间（-0,0),(0,+)(3)当 xE(-0,0) 时, f'(x)>0当 xE(0,+o)时,f(x)>0 .故函数f(x)=3/x在(-00,+80)上单调增加

6 3 判断函数 f (x)  x的单调性. （1）定义域为 (,) 2 3 1 ( ) 3 f x x  (2)   , 3 f (x)  x在点x  0处导数不存在. 点 x  0 把定义域分成两部分区间 (,0),(0,) . (3)当 x(,0) 时， f (x)  0 当 x(0,)时， f (x)  0 . 3 故函数 f (x)  x在(,)上单调增加. 解 例 2 01 函数的单调性

01函数的单调性OOAO人邮教育判断函数 f(x)=2-(x2-1)的单调性例3f(x)=2-(x2-1)3 的定义域为(80,+0),解(1)4.2-1)3,f(x)=-4x1L(2)则f(x）的驻点为x=0，在点x=±1处导数不存在(3)当 xE(-80,-1)和(0,1)时,f(x)>0 ;当xE(-1,0)和(1,+o) 时,f'(x)<0 .故函数f(x)=2-(x2-1)3在(-00,-1)和(0,1)上单调增加;在[-1,0]和[1,+o0)上单调减少

7 2 2 3 判断函数 f (x)  2(x 1) 的单调性. f (x)  0； f (x)  0 . 解 例 3 01 函数的单调性 (1) 的定义域为 (,)， 2 2 3 f (x)  2(x 1) ， 1 2 3 4 1 3 ( ) ( ) x f x x  (2)     则 f (x) 的驻点为x  0 ，在点x  1 处导数不存在. (3)当 x(,1) 和 (0,1) 时， 当x(1,0)和 (1,) 时， 故函数 在 2 2 3 f (x)  2(x 1) (,1) 和 (0,1) 上单调增加； 在 [1,0]和 [1,)上单调减少

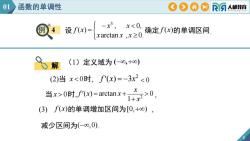
01函数的单调性OOAO人邮教育x0当x>0时,f'(x)=arctanx+1+ x(3）f(x)的单调增加区间为[0,+）减少区间为(-8,0)

8 3 , 0, ( ) arctan , 0. x x f x x x x        设 确定 f (x)的单调区间. x  0 2 (2)当 时, f (x)  3x x  0 2 ( ) arctan 0 1 x f x x x      当 时, , (3) f (x)的单调增加区间为[0,) , 减少区间为(,0). 解 例 4 01 函数的单调性 （1）定义域为 (,)  0

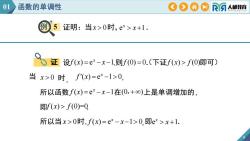
01函数的单调性CO0RA人邮教育例5证明：当x>0时，e">x+1.Q 证设f(x)=e-x-1,则f(0)=0.(下证f(x)>f(0)即可)当 x>0 时。f'(x)=e*-1>0,所以函数f(x)=e-x-1在(O,+o0)上是单调增加的即f(x)> f(O)=0所以当x>0时,f(x)=e-x-1>0,即e>x+1

9 x  0 e 1 x 证明：当 时，  x  ． ( ) e 1 x 设f x   x  ,则f (0)  0． 当 x  0 时 , ( ) e 1 0 x f  x    , ( ) e 1 x 所以函数 f x   x  在(0，)上是单调增加的, 即f (x)  f (0)=0． 所以当 x  0时, ( ) e 1 0 x f x   x  , e 1 x 即  x  ． （下证f (x)  f (0)即可） 例 5 证 01 函数的单调性

R人邮教育本讲内容w.nyjiaoyu.co01函数的单调性02函数的极值03函数的最值

01 函数的单调性 02 函数的极值 03 函数的最值 本 讲 内 容