《高等数学》课程教学资源（课件讲稿）第1章——第3节函数极限的定义与性质

第一章第二节函数极限的定义自变量趋于无穷大时函数的极限一、目二、自变量趋于有限值时函数的极限函数极限的性质一、HIGHEDUCATIONPRESS机动目录上页下页返回结束

第一章 二、自变量趋于有限值时函数的极限 第二节 一、自变量趋于无穷大时函数的极限 机动 目录 上页 下页 返回 结束 函数极限的定义 三、函数极限的性质

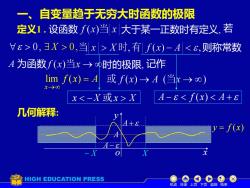
一、目自变量趋于无穷大时函数的极限定义1.设函数f(x)当x|大于某一正数时有定义,若>0,X>0,当 x|>X时,有f(x)-AX几何解释：Atay= f(x)0XHIGH EDUCATION PRESS机动目录上页下页返回结束

− X X A +  A −  o x y y = f (x) A 一、自变量趋于无穷大时函数的极限 定义1 . 设函数 大于某一正数时有定义, 若  X  0, 则称常数 时的极限, f x A x = → lim ( ) 几何解释: x  −X 或x  X A −   f (x)  A +  记作   0, 机动 目录 上页 下页 返回 结束 A 为函数

例.证明limx-00 xX证：故ε>0,欲使X时,就有CX因此limx→0 xHIGH EDUCATION PRESS机动目录上页下页返回结束

例. 证明 0. 1 lim = x→ x 证: 0 1 − x x 1 = 取 , 1  X = 因此 就有 故   0, 欲使 即 o x y x y 1 = 机动 目录 上页 下页 返回 结束

两种特殊情况：lim f(x)=Aε>0,3X>0,当 x>X时,有x→+00f(x)-A0,X>0,当x<-X时,有x-00f(x)-A<8lim f(x)= A= lim f(x)lim f(x)= Ax→-8X→+80x0HIGH EDUCATION PRESS机动目录上页下页返回结束

两种特殊情况 : f x A x = →+ lim ( )   0,  X  0, 当 时, 有 f (x) − A     0,  X  0, 当 x  −X 时, 有 f (x) − A   机动 目录 上页 下页 返回 结束 lim ( ) lim ( ) x x f x A f x →− →+ = =

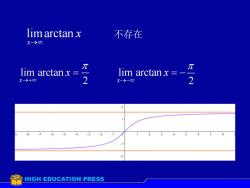
lim arctan x不存在x-8元元lim arctan x :lim arctan x =22x→+o0X→-0-6-5-4-3-256-74-8-13HIGH EDUCATION PRESS

limarctan x x → lim arctan x 2 x  →− lim arctan = − x 2 x  →+ = 不存在

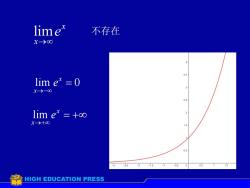
limex不存在x-→83.5lim e* = 03X--802.52lim e":=+8X-→+81.50.52.5-2-10.50.5-1.501.5-3HIGHEDUCATION PRESS

lim x x e → 不存在 lim 0 x x e →− = lim x x e →+ = +

二、I自变量趋于有限值时函数的极限1. x → xo时函数极限的定义测量正方形面积.（真值：边长为xo;面积为A）引例直接观测值确定直接观测值精度S边长x<x-Xo间接观测值x2-A<8任给精度ε，要求+2面积AXoHIGH EDUCATIONPRESS机动目录上页下页返回结束

二、自变量趋于有限值时函数的极限 1. 时函数极限的定义 引例. 测量正方形面积. (真值: 边长为 面积为A ) 边长 面积 直接观测值 间接观测值 任给精度  , 要求 x − A   2 确定直接观测值精度  : x − x0   0 A x 机动 目录 上页 下页 返回 结束

定义2.设函数,f(x)在点 xo 的某去心邻域内有定义若>0,38>0,当 00, 3S>0,当xEU(xo,S)即x-→xo时,有|f(x)-A|<c几何解释：yzf(x)A+εAA-Xo-S xoxo+8 xHIGH EDUCATION PRESS机动目录上页下页返回结束

定义2 . 设函数 在点 的某去心邻域内有定义 ,   0,   0, 当  −   0 0 x x 时, 有 f (x) − A   则称常数 A 为函数 当 时的极限, f x A x x = → lim ( ) 0 或 即 当 时, 有 若 记作 几何解释: +  0 x A +  A −  A x0 x y y = f (x) 机动 目录 上页 下页 返回 结束

例.证明lim C=C（C为常数x→xo证：f(x)-A=C-C=0故>0,对任意的>0,当0<|-xo时总有C-C=0<8因此lim C= Cx→xoHIGH EDUCATION PRESS机动目录上页下页返回结束

例. 证明 证: f (x) − A 故   0, 对任意的   0, 当 时 , 因此 总有 机动 目录 上页 下页 返回 结束

例.证明lim(2x -1) = 1x>1证：f(x)-A=(2x-1)-1=2x-11x-10,欲使/f(x)-A<ε,只要8则当 0<|x-1|< 时,必有取=f(x)-A=(2x-1)-1<8因此lim(2x -1) =1x→1HIGH EDUCATION PRESS机动目录上页下页返回结束

例. 证明 证: = 2 x −1   0, 欲使 取 , 2   = 则当 0  x −1   时 , 必有 因此 只要 机动 目录 上页 下页 返回 结束