《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第七节

第三章曲率第七节弧微分曲率二、三、曲率半径与曲率圆HIGHEDUCATION PRESS机动目录上页返回下页结束

第七节 机动 目录 上页 下页 返回 结束 一、 弧微分 二、 曲率 三、 曲率半径与曲率圆 曲率 第三章

曲线的弯曲程度与切线的转角有关与曲线的弧长有关MAaHIGHEDUCATION PRESS机动目录上页返回下页结束

曲线的弯曲程度 与切线的转角有关 与曲线的弧长有关 机动 目录 上页 下页 返回 结束  M  M M  M M  P P

在光滑弧上自点 M开始取弧段,其长为△s，对应切线转角为△α，定义弧段△S上的平均曲率NaKMMAr点M处的曲率daAaK = limA5-0注意：直线上任意点处的曲率为0！HIGH EDUCATION PRESS机动目录上页下页返回结束

在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线  , 定义 弧段 s 上的平均曲率 s K   =   M M  s 点 M 处的曲率 s K s   =  →  0 lim ds d = 注意: 直线上任意点处的曲率为 0 ! 机动 目录 上页 下页 返回 结束 转角为

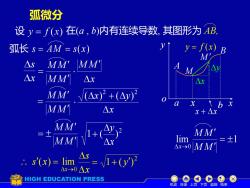
弧微分AB设 = f(x)在(α,b)内有连续导数, 其图形为Vy= f(x)弧长 s= AM = s(x)BMMMAsMM'VAxMMAXAxMM(△x)? +(△y)xbxQMM'△xx+△xMM'MM'lim=±1MM'MM'Ax-→0= /1+(y)3s(x)= limAx-→0 AxHIGH EDUCATION PRESS机动目录上页下页返回结束

弧微分 设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s = AM = s( x) x s   M M M M   = x M M    M M M M   = x x y   +   2 2 ( ) ( ) M M M M   =  2 1 ( ) x y   + x s s x x     =  →0 ( ) lim 2 = 1+ ( y ) x A B y = f (x) a b x o y x M x + x M  y lim 1 0 =     → M M M M x 机动 目录 上页 下页 返回 结束

s(x)= 1+(y)3ds = /1+(y)?dx 或 ds = /(dx) +(dy)2x= x(t)若曲线由参数方程表示(y= y(t)则弧长微分公式为V(x) +(v)* d tds =几何意义：ds =|MTayMdxdxQ= sinα= cosα ;dsdsx x+dxxOHIGH EDUCATION PRESS机动目录上页下页返回结束

则弧长微分公式为 ( ) ( ) 2 2 d d s x y t = +   ds 1 ( y ) dx 2  = +  或 2 2 ds = (dx) + (dy) x + dx dx o x y x M dy T  几何意义: ds = MT cos ; d d =  s x sin d d = s y 若曲线由参数方程表示:    = = ( ) ( ) y y t x x t 机动 目录 上页 下页 返回 结束

曲率K的计算公式dαK=设曲线弧y=f(x)二阶可导ds(设-至tanα = y'得α = arctan ydxdα = (arctan y)'dx+1又ds = 1 + y'? dx故曲率计算公式为K=(1 + y*2)%HIGH EDUCATION PRESS机动目录上页下页返回结束

tan = y  ) 2 2 (    设 −   得  = arctan y  d = (arctan y )dx 故曲率计算公式为 s K d d = 2 3 (1 ) 2 y y K +   = 又 曲率K 的计算公式 设曲线弧 y = f (x) 二阶可导, 机动 目录 上页 下页 返回 结束

例.求半径为R的圆上任意点处的曲率解：如图所示M△s=R△ααAsR~~AaK = limVR△s0As可见：R愈小，则K愈大，圆弧弯曲得愈厉害R愈大，则K愈小，圆弧弯曲得愈小HIGH EDUCATION PRESS机动目录上页下页返回结束

例. 求半径为R 的圆上任意点处的曲率 . 解: 如图所示 , s = R s K s    =  →  0 lim R 1 = 可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ; R 愈大, 则K 愈小 , 圆弧弯曲得愈小 .  s R M M   机动 目录 上页 下页 返回 结束

说明：x = x(t)给出,则(1)若曲线由参数方程y=y(t)x'y"-x"y'((x) +(y)")%(2)若曲线方程为 x=β(y),则K=(1+ x*2)2K=(1+ y2)%HIGH EDUCATION PRESS机动目录上页下页返回结束

说明: (1) 若曲线由参数方程    = = ( ) ( ) y y t x x t 给出, 则 2 3 (1 ) 2 y y K +   = (2) 若曲线方程为 x =  ( y), 则 2 3 (1 ) 2 x x K +   = ( ) ( ) 3 2 2 2 ( ) x y x y K x y     − =   + 机动 目录 上页 下页 返回 结束

例计算等边双曲线xy=1在点(1.1)处的曲率例 抛物线 y=ax2+bx+c(a0)哪一点的曲率最大?HGHEDUCATION PRESS

第七节 曲率 第三章 微分中值定理与导数的应用 例 ( ) 2 例 抛物线 y ax bx c a = + +  0

曲率半径与曲率园D(α, β)设 M为曲线 C上任一点，在点在曲线M处作曲线的切线和法线TR的凹向一侧法线上取点D使M(x,y)1xDM=R=K把以D为中心，R为半径的圆叫做曲线在点M处的D叫做曲率中心曲率圆（密切圆），R叫做曲率半径在点M处曲率圆与曲线有下列密切关系(2)凹向一致；(1）有公切线(3)曲率相同HIGHEDUCATIONPRESS机动目录上页下页返回结束

曲率半径与曲率园 T y o x D( ,  ) R M (x, y) C 设 M 为曲线 C 上任一点 , 在点 在曲线 K DM R 1 = = 把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的 曲率圆 ( 密切圆 ) , R 叫做曲率半径, D 叫做曲率中心. 在点M 处曲率圆与曲线有下列密切关系: (1) 有公切线; (2) 凹向一致; (3) 曲率相同 . M 处作曲线的切线和法线, 的凹向一侧法线上取点 D 使 机动 目录 上页 下页 返回 结束