《高等数学》课程教学资源（课件讲稿）第二章_2.3

第四节隐函数及由参数方程所确定的函数的导数隐函数的导数、二、 E由参数方程所确定的函数的导数三、小结思考题高等数学（上册）

一 、隐函数的导数 三、小结 思考题 二、由参数方程所确定的 函数的导数 第四节 隐函数及由参数方程 所确定的函数的导数

一、隐函数的导数(differentiation of functions represented implicitly)定义：由方程F(x,)=O所确定的函数=(x)称为隐函数y=f(x)形式称为显函数，F(x,y)=0 →隐函数的显化y=f(x)高等数学（上册）

一、隐函数的导数 定义: . ( , ) 0 ( ) 称为隐函数 由方程F x y  所确定的函数 y  y x y  f (x) 形式称为显函数. F(x, y)  0 y  f (x) 隐函数的显化 (differentiation of functions represented implicitly)

例如，都是显函数y=sinx,y=lnx+/1-x?,y=xlnx/1-sinx方程x+y3-1=0 能确定一个隐函y=f(x) 它能显化：数y=3/1-x.开普勒方程=x+sin(O<<l)能确定一个隐函数=f(x),但无法将y表达成x的显式表达式.不能显化开普勒J.Kepler）1571-1630德国数学家，天文学家高等数学（上册）

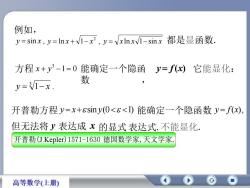
例如， y  sin x , ln 1 , 2 y  x   x y  x ln x 1 sin x 都是显函数. 方程 1 0 3 x  y   它能显化： 1 . 3 y   x 开普勒方程 y  x sin y(0 1) 但无法将 y 表达成 x 的显式 表达式.不能显化. 开普勒(J.Kepler)1571-1630 德国数学家,天文学家. 能确定一个隐函数 y  f(x), 能确定一个隐函 数 ， y  f(x)

问题：隐函数不易显化或不能显化如何求导？隐函数求导法则：用复合函数求导法则直接对方程两边求导并注意到其中变量V是x的函数高等数学（上册）

问题:隐函数不易显化或不能显化如何求导? 隐函数求导法则: 用复合函数求导法则直接对方程两边求导. 并注意到其中

例1 求由方程呈xy-ex+e=0所确定的隐函数dy, dyy的导数1x=0dx'dx解方程两边对x求导dy01y+xdxdxex-ydy解得x=0代入原方程=y=0x+eydxdyey=1.-x=0x=0esdxx+y=0高等数学（上册）

例1 . d d , d d 0 0    x x y x y x y y xy e e 的导数 求由方程 所确定的隐函数 解 方程两边对x求导, 0 d d d d     x y e e x y y x x y 解得 , d d y x x e e y x y    x  0代入原方程  y  0, 0 0 0 d d        y y x x x x e e y x y  1

例2设曲线C的方程为x3+y3=3xy,求过C上.33点(的切线方程，并证明曲线C在该点的法?线通过原点.高等数学（上册）

. ) , 2 3 , 2 3 ( 3 , 3 3 线通过原点 点 的切线方程 并证明曲线 在该点的法 设曲线 的方程为 求过 上 C 例2 C x  y  xy C

例2设曲线C的方程为x3+y3=3xy,求过C上点(的切线方程，并证明曲线C在该点的法线通过原点。解方程两边对x求导，3x2+3y2y'=3y+3xy"-x3元-1.3.3X222733即x+y-3=0.所求切线方程为2233法线方程为即显然通过原点y=x,22高等数学（上册）

例2 . ) , 2 3 , 2 3 ( 3 , 3 3 线通过原点 点 的切线方程 并证明曲线 在该点的法 设曲线 的方程为 求过 上 C C x  y  xy C 解 方程两边对x求导, 3x  3 y y  3 y  3xy 2 2 ) 2 3 , 2 3 ( 2 2 ) 2 3 , 2 3 ( y x y x y       1. 所求切线方程为 ) 2 3 ( 2 3 y    x  即 x  y  3  0. 2 3 2 3 法线方程为 y   x  即 y  x, 显然通过原点

求隐函数=x)的二阶导数"的方法法1或：先求出一阶导，再对一阶导的结果求导法2把y看成 x 的函数，方程两边同时对x求两次导代入，得到高等数学（上册）

求隐函数 y  y(x) 的二阶导数 y  的方法: 方程两边同时对 x 求两次导, 把 y 看成 x 的函数， 代入y  ， 得到 y  . 或：先求出一阶导 y  ，再对一阶导 y  的结果求导 法2 法1

0000求由方程x+sin=0所确定的隐函数y=(x)的二阶导数2解方程两边对x求导，得1-+=cosy·y=022解得y=2-cos y2-2sin y.y代入得上式两边再对x求导，y"=再将y2-cOSy(2 -cos y)-4siny2"(2 -cOs y)高等数学（上册）

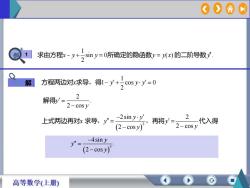
9 1 sin 0 ( ) . 2 求由方程x  y  y  所确定的隐函数y  y x 的二阶导数y  1 1 cos 0 2 方程两边对x求导，得  y   y  y   例 1 解   2 2sin 2 2 cos 2 cos y y x y y y y          上式两边再对 求导， ，再将 代入得 2 . 2 cos y y    解得   3 4sin . 2 cos y y y    

例3设x4-xy+y4=1,求y"在点(0,1)处的值解?方程两边对x求导得(1)4x - y-xy'+4yy= 0代入x=0,y=1得x=0 =J=1(y)=yy",dyd2dx?dx dx将方程(1)两边再对x求导得12x? - y' -(y' +xy")+ 4[3y"y'y' + y"y3] = 012x2 - 2y'- xy" + 12 y(y')° + 4y"y" = 01代入x=0,y=1,J得x=016V=1y=l6高等数学（上册）

例3 1, (0,1) . 设 x 4  xy  y 4  求y在点 处的值 解 方程两边对x求导得 4 4 0 (1) 3 3 x  y  xy  y y  代入 x  0, y  1得 ; 4 1 1  0    y x y 将方程(1)两边再对x求导得 12 2 12 ( ) 4 0 2 2 2 3 x  y  xy  y y  y y  得4 1 1  0    y x 代入 x  0, y  1, y . 16 1 1  0     y x y 2 2 2 = dy dy d y y y y y dx dx dx （ ）    ，  2 2 3 12x  y   ( y   xy )  4[3y y .y   y  y ]  0