《高等数学》课程教学资源（课件讲稿）第三章_3.4.1

第三节导数的应用函数的单调性小结思考题高等数学（上册）

函数的单调性 第三节 导数的应用 小结 思考题

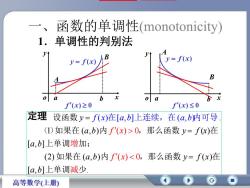
函数的单调性(monotonicity)一1.单调性的判别法1-yyBy= f(x)y= f(x)BAbx0bxa0af'(x)≥ 0f'(x)≤0定理设函数y= f(x)在[a,b]上连续，在(a,b)内可导(1)如果在(a,b)内 f'(x)>0，那么函数 y= f(x)在[a,b]上单调增加;(2)如果在(a,b)内f'(x)<0, 那么函数 y= f(x)在[a,b]上单调减少高等数学（上册）

一、函数的单调性(monotonicity) x y o y  f (x) x y o y  f (x) a b A B f (x)  0 f (x)  0 定理 1 ( , ) ( ( ) [ , ] (2 ( ) [ , ] ( , ) . ) 0 ) ( , ) ( ) 0 ( ) [ , ] . f x y a b y f f x f x a b a b x a b a b y f x a b        设函数 （）如果在 内 ，那么函数 在 在 上连续，在 内可导 上单调增加； 如果在 内 ，那么函数 在 上单调减少 a b B A 1．单调性的判别法

证xi,x, E(a,b), 且 x, 0,若在(a,b)内，f'(x)> 0,则 f'() > 0,: f(x2)>f(x). y=f(x)在[a,b]上单调增加若在(a,b)内，f'(x)<0,则 f()< 0,:. f(x2)< f(x). : y= f(x)在[a,bl]上单调减少C高等数学（上册）

证 , ( , ), 1 2  x x  a b , 1 2 且 x  x 应用拉氏定理,得 ( ) ( ) ( )( ) ( ) 2 1 2 1 1 2 f x  f x  f   x  x x    x 0,  x2  x1  若在(a,b)内，f (x)  0, 则 f ( )  0, ( ) ( ). 2 1  f x  f x  y  f (x)在[a,b]上单调增加. 若在(a,b)内，f (x)  0, 则 f ( )  0, ( ) ( ). 2 1  f x  f x  y  f (x)在[a,b]上单调减少

例1 讨论函数y=e＊-x-1的单调性解 定义域为(-80,+8)： y' = e* -1. 在(-00,0)内, y'0,:函数在[0,+8)单调增加高等数学（上册）

例1 解 讨论函数y  e  x  1的单调性. x    1. x  y e 在(,0)内, y  0, 函数在(,0]单调减少； 在(0,)内, y  0, 函数在[0,)单调增加. 定义域为(,)

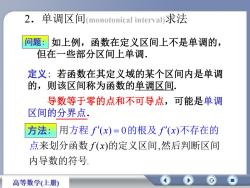
2.．单调区间(monotonical interval)求法问题：如上例，函数在定义区间上不是单调的，但在一些部分区间上单调。定义：若函数在其定义域的某个区间内是单调的，则该区间称为函数的单调区间导数等于零的点和不可导点，可能是单调区间的分界点。方法：用方程f'(x)=0的根及f'(x)不存在的点来划分函数f(x)的定义区间,然后判断区间内导数的符号高等数学（上册）

2．单调区间(monotonical interval)求法 如上例，函数在定义区间上不是单调的， 但在一些部分区间上单调． 定义: 若函数在其定义域的某个区间内是单调 的，则该区间称为函数的单调区间. 导数等于零的点和不可导点，可能是单调 区间的分界点． 方法: ( ) , ( ) 0 ( ) . f x 用 f  x  f  x 来划分函数 的定义区间 然后判断区 方程 的根及 不存 间 内导数 在 点 的符号 的 问题:

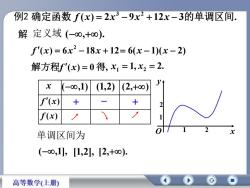
例2确定函数f(x)=2x3-9x2+12x-3的单调区间解 定义域(-80,+8),f'(x) = 6x2 -18x + 12= 6(x - 1)(x - 2)解方程f'(x)= 0 得,x, =1,x2 = 2.Vx(1,2)(2,+8)(-8,1)f'(x)++2f(x)1f2x单调区间为(-00,1],[1,2], [2,+80),高等数学（上册）

例2 解 ( ) 2 9 12 3 . 确定函数 f x  x 3  x 2  x  的单调区间 ( ) 6 18 12 2 f  x  x  x   6(x  1)(x  2) 解方程f (x)  0 得, 1, x1  2. x2  定义域 (,). x (,1) (1,2) (2,) f (x) f (x)    单调区间为 (,1], [1,2], [2,). x y O 1 1 2 2

例3确定函数 f(x)=/x2的单调区间。yt解定义域(-80,+o).y=/x?2f'(x)(x# 0):3/xolx当x=0时,导数不存在x1(-80,0)(0,+8)f'(x)+f(x)71单调区间为(-80,0],[0,+),高等数学（上册）

例3 解 ( ) . 确定函数 f x  3 x 2 的单调区间 , ( 0) 3 2 ( ) 3   x  x f x 当x  0时, 单调区间为 (,0], [0,). 3 2 y  x 导数不存在. x (,0) (0,) f (x) f (x)   定义域 (,). x y O

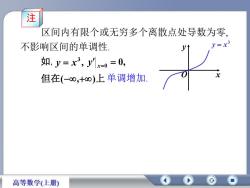
注区间内有限个或无穷多个离散点处导数为零y=x3不影响区间的单调性V如, = x3, x=o = 0,x但在(-80,+8)上单调增加高等数学（上册）

区间内有限个或无穷多个离散点处导数为零, 如, , 3 y  x 0, y x0  但在(,)上 注 不影响区间的单调性.单调增加. 3 y  x x y O

3.利用单调性证明不等式例4 当x>0时,试证x>In(1+ x)成立x证 设f(x)=x-ln(1+x)， 则 f'(x)=1+x： f(x)在[0,+o)上连续,且在(0,+o)可导，f(x)>0,; : f(0) =0,：在[0,+o)上单调增加;:. 当x>0时,f(x)>f(0)=0,x -ln(1+ x) > 0即 x >In(1 + x)高等数学（上册）

例4 证 当x  0时,试证x  ln(1  x)成立. 设f (x)  x ln(1 x), . 1 ( ) x x f x  则   在[0,)上单调增加；  f (0)  0, 3．利用单调性证明不等式  f (x)在[0,)上连续,且在(0,)可 导， f ( x)  0, 当x  0时， x  ln(1 x)  0, 即 x  ln(1  x). f ( x)  f (0)  0