《高等数学》课程教学资源（课件讲稿）第一章_1.3.2-1.3.4

第五节极限存在准则连续复利两个重要极限一、夹逼准则二、单调有界收敛准则三、连续复利四、小结思考题高等数学（上册）

一 、夹逼准则 二、单调有界收敛准则 四、小结 思考题 极限存在准则 两个重要极限 第五节 三、连续复利 连续复利

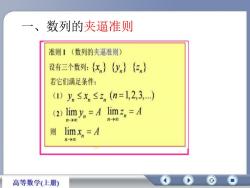
一、数列的夹逼准则准则！（数列的夹逼准则）设有三个数列：（x）(y（z,）若它们满足条件：(1)y,≤x,≤z,(n=1,2,3..)limy,=A limz,=A(2）n-+on-00则limx,=An-+00高等数学（上册）

一、数列的夹逼准则

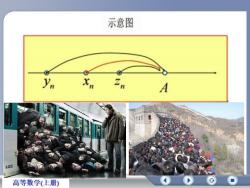
示意图ynxZAHHN.4056高等数学（上册）

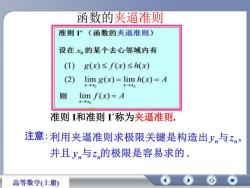
函数的夹逼准则准则I（函数的夹逼准则）设在的某个去心邻域内有1)g(x)≤f(x)≤h(x)(2)limg(x)=limh(x)=Ax-→xoX-→XD则limf(x)=AX-→30准则和准则I称为夹逼准则注意：利用夹逼准则求极限关键是构造出y,与zn并且,与z,的极限是容易求的。高等数学（上册）

注意: . , 并且 与 的极限是容易求的 利用夹逼准则求极限关键是构造出 与 n n n n y z y z 准则 I和准则 Iˊ称为夹逼准则. 函数的夹逼准则

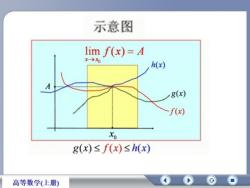
示意图lim f(x)=AX-→xoh(x)g(x)f(x)Xog(x)≤f(x)≤h(x)高等数学（上册）

111例1 求 lim(2n2+222+1n→0Inn'+n11nn解Vn?n2+1+1+n+nnT又 limlim21n08+nn1 +n1nlimlim由夹逼定理得11n>+1n>心n111lim(22+2n-0+1n+nO高等数学（上册）

例1 ). 1 2 1 1 1 lim( 2 2 2 n n n n  n       求  解 , 1 1 1 1 2 2 2 2         n n n n n n n n   n n n n n n 1 1 1 lim 2 lim      又  1, 2 2 1 1 1 lim 1 lim n n n n n       1, 由夹逼定理得 ) 1. 1 2 1 1 1 lim( 2 2 2       n n  n n n 

21n求lim(例.+n+2n>0+n+lnnn+n+nS21n角解记xn?+n+1n?+n+2n-+n+n将x,放缩得21+2+..+n1+2+...+nn≤x.<nn?+n+nn?+n+1-n+i+n+nn6高等数学（上册）

例 解 2 2 2 1 2 lim( ). n 1 2 n  n n n n n n n         求 ＋  2 2 2 1 2 1 2 n n x n n n n n n n          记 ＋  ， n 将x 放缩得 2 2 2 2 2 1 2 1 2 1 2 1 1 1 1 n n n n x n n n n n n n n n n n                        ＋ 

接n(n +1)11+2+...+n2而 limlim2'n?+n+n.n-00n>0n'+n+nn(n+ 1)11+2+...+n2limlimn2+n+1n-→ n? + n+12n-→001即根据夹逼准则得，limx2nn->021国nlim(2n?+n+2+n+1n→nn+n+nC高等数学（上册）

接 前 2 2 2 1 2 1 lim( )= . n 1 2 2 n  n n n n n n n         ＋  2 2 ( 1) 1 2 1 2 lim lim n n 2 n n n  n n n  n n n            而 ， 2 2 ( 1) 1 2 1 2 lim lim n 1 n 1 2 n n n  n n  n n            ， 1 lim = 2 n n x  根据夹逼准则得， ，即

作为准则I'的应用，得到下面一个重要的极限：sinx0型是lim0x-→0x(x→0)sinx~x0注：归纳本质sin(是型lim100-sin例如：x=1，有时会用到代换limX-+00x高等数学（上册）

作为准则Ⅰ´的应用，得到下面一个 重要的极限： 1 sin lim 0   x x x sin x  x (x0) 例如： ，有时会用到代换. 注：归纳本质： ( ) 0 ( ) 0 ( sin lim ) 0 1   是 型

sinxlimx→0x0x型例2求 lim0x-0sinx1解 原式=limsinxx>0x1sin xlimx-→0xx所以limx-→0 sinx高等数学（上册）

例2 0 lim . x sinx  x 求 0 1 limx sin x x  解 原式  0 1sin limx x  x  1 1 1   0 lim =1 x sinx  x 所以