《高等数学》课程教学资源（课件讲稿）第三章_3.6

第六节曲率(curvature)弧微分(arc element)曲率及其计算公式曲率圆与曲率半径小结作业思考题第三章 微分中值定理与导数的应用高等数学（上册）

第六节 曲 率 弧微分 曲率及其计算公式 曲率圆与曲率半径 小结 思考题 作业 (curvature) (arc element) 第三章 微分中值定理与导数的应用

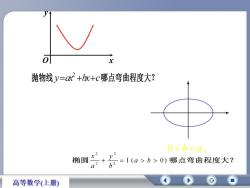
x抛物线y=ax2+bx+c哪点弯曲程度大?0b>0）哪点弯曲程度大？Q62高等数学（上册）

y x b a b  a 0  b  a , x yO

回顾旧知：微分dy = f"(x)dx.高等数学（上册）

回顾旧知： 微分dy  f (x)dx

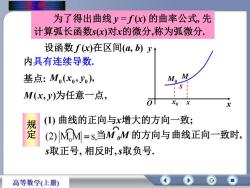
西为了得出曲线y=f(x）的曲率公式，先计算弧长函数s(x）对x的微分，称为弧微分设函数f(x)在区间(a,b) y内具有连续导数M基点: M.(xo,yo),M.M(x,y)为任意一点tXoxx(1)曲线的正向与x增大的方向一致;规定(2)M,M =s,当M M 的方向与曲线正向一致时,s取正号，相反时，s取负号高等数学（上册）

曲 率 一 、弧微分 为了得出曲线 y = f (x) 的曲率公式, 先 计算弧长函数s(x)对x的微分,称为弧微分. ( , ), 0 0 0 M x y M(x, y)为任意一点, (2) M M s, 0  s取正号, 规 定 相反时,s取负号. 设函数 f (x)在区间(a, b) 内具有连续导数. 基点: (1) 曲线的正向与x增大的方向一致; ⌒ 当M 0M 的方向与曲线正向一致时, x y O s x M x0 M0 

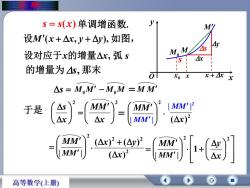
摩ys = s(x)单调增函数.M/设M'(x +Ax,y+Ay),如图,4y4sM. M设对应于x的增量Ax.弧 sAxIS的增量为 4s,那末tx+zxxoxAs = M,M' -M,M =MM'IMM'-{MMMM'AS于是会格2(Ar)2AxIMM'IMM(Ax)~ +(Ay)?()[()MM'(Ax)2MMT源高等数学（上册）

s  s(x)单调增函数. 设M(x  x, y  y), 如图， 曲 率 设对应于x的增量x, s, s  M M 0  M0M  M M 于是          2 x s 2         x MM  2 (x)         2 MM | MM | 2 | MM | 2         MM | MM | 2 2 2 ( ) ( ) ( ) x x y      2         MM | MM |               2 1 x y 弧 s 的增量为 那末 x y O s x M x0 M0 x  x M s x y

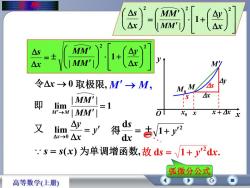
摩(））（）e中土1ArM4y令△x→0 取极限,M'→M.AsM. M4xHSMM'即lim=1tM'-→Mx+zxIMM'XoxxAyds又/1+ y'2得lim士Ax→0Ardx：s= s(x)为单调增函数,故 ds = /1+y'dx弧微分公式高等数学（上册）

曲 率    x s 2         x s 2         MM | MM |               2 1 x y 令x  0 取极限, M  M,                        2 2 1 | | x y MM MM | | | | lim MM MM M M    即  1 又 y x y x      0 lim 得  x s d d d 1 d . 2 故 s   y x 弧微分公式 2  1 y  s  s(x) 为单调增函数, x y O s x M x0 M0 x  x M s x y

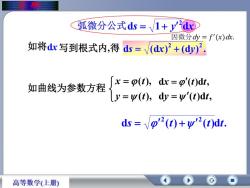
摩弧微分公式ds=/1+y'dx因微分dy=f(x)dx如将dx写到根式内,得ds = /(dx)" + (dy)x = p(t), dx =β'(t)dt,如曲线为参数方程y = y(t), dy = y'(t)dt,ds = p'(t)+ y'?(t)dt.高等数学（上册）

如将 d (d ) (d ) . 2 2 s  x  y dx  (t)dt, d ( ) ( )d . 2 2 s   t  t t 曲 率 ds 1 y dx 2 弧微分公式     dy (t)dt,     ( ), ( ), y t x t   如曲线为参数方程 dx写到根式内,得

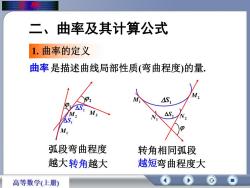
摩二、曲率及其计算公式1.曲率的定义曲率是描述曲线局部性质(弯曲程度)的量M2P24S,MPASM,MzASN2NASM,弧段弯曲程度转角相同弧段越大转角越大越短弯曲程度大高等数学（上册）

是描述曲线局部性质(弯曲程度)的量. 弧段弯曲程度 越大 转角相同弧段 越短 1. 曲率的定义 曲 率 曲率 转角越大 弯曲程度大 二、曲率及其计算公式 M1 M2 M3 1  2 S1 S2 M1 M2 N1 N2  S1 S2

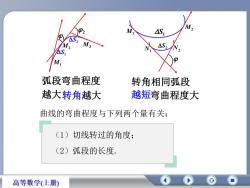
M202M4S,oAS,M,AS,MN2NAS@M,弧段弯曲程度转角相同弧段越大转角越大越短弯曲程度大曲线的弯曲程度与下列两个量有关：（1）切线转过的角度；（2）弧段的长度高等数学（上册）

曲线的弯曲程度与下列两个量有关： （1）切线转过的角度； （2）弧段的长度. 弧段弯曲程度 越大 转角相同弧段 转角越大 越短弯曲程度大 M1 M2 M3 1  2 S1 S2 M1 M2 N1 N2  S1 S2

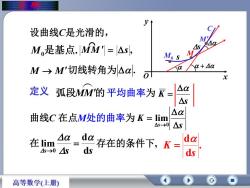
摩y设曲线C是光滑的，M'a4sM,是基点.MM=|△sl,MM. sα+4αaM→M'切线转角为△αl.可xAα定义弧段MM'的平均曲率为斥AsAα曲线C在点M处的曲率为K= limAsAs-0Aαdαda在 lim存在的条件下，K：4sds4s→0ds高等数学（上册）

s K     设曲线C是光滑的， . M0是基点 M  M 定义 s K s       0 曲线C 在点M处的曲率为 lim s s ds d lim 0       在 . d d s K   曲 率 MM   s , ⌒ 切线 （ 转角为  . 弧段MM的平均曲率为 存在的条件下, x y O s s  C     M0 M M