《高等数学》课程教学资源（课件讲稿）第三章_3.4.2

第三节导数的应用函数的极值小结思考题高等数学（上册）

函数的极值 第三节 导数的应用 小结 思考题

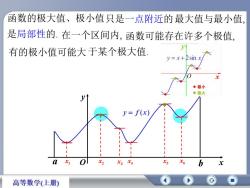
函数的极大值、极小值只是一点附近的最大值与最小值是局部性的.在一个区间内，函数可能存在许多个极值有的极小值可能大于某个极大值y=x+sinxx·极小极大6y=f(x)olX6X2baXiXsX3Xx高等数学（上册）

x1 x2 x3 x4 x5 x6 函数的极大值、极小值 是局部性的. 在一个区间内, 函数可能存在许多个极值, 最大值与最小值, 有的极小值可能大 于某个极大值. 只是一点附近的     x y a O b y  f ( x)  

使导数f(x)为零的点叫做函数f(x)的驻点极值的必要条件2极值点驻点定理1(必要条件)1.如果函数f(x)在点x,处取得极值,且在x,处可导,则必有f(x)=0注（(1)可导函数的极值点必是驻点，但函数的J=x3驻点却不一定是极值点y如, y=x3, |x=0 = 0,x但x=0不是极值点高等数学（上册）

定理1(必要条件) 注 如, , 3 y  x 0, y x0  但x  0不是极值点. (1) 如果函数f ( x)在点x0处取得 , 且在x0处可导 叫做函数 的 使导数 为零的点 ( ) ( ) f x f  x 驻点. 可导函数的极值点 驻点却不一定是极值点. 但函数的 2. 极值的必要条件 必是驻点, 0 极值, 则必有f (x )  0. 3 y  x x y O 极值点驻点

(2)极值点也可能是导数不存在的点Dy=/x?如，=2,x=0是极小值点但=x2在x=0不可导0x高等数学（上册）

x yO 3 2 y  x 极值点也可能是导数不存在的点. 如, , 3 2 y  x 3 2 但 y  x (2) 不可导. x  0 是极小值点.  在x  0

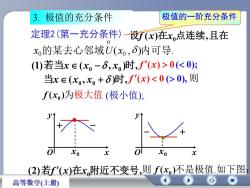
极值的一阶充分条件极值的充分条件3定理2(第一充分条件)一设f(x)在x,点连续,且在xo的某去心邻域U(xo,)内可导(1)若当x E (x。-S,x)时,f'(x)>0( 0),则f(x)为极大值 (极小值);yyototxoxoxx(2)若f(x)在x,附近不变号,则f(x)不是极值.如下图高等数学（上册）

定理2(第一充分条件) 设f (x)在x0点连续,且在 (1) ( , ) , 若当x  x0   x0 时 f (x)  0( 0); ( , ) , 当x  x0 x0   时 f (x)  0 ( 0), 则 ( ) x0 f 为极大值 (2) ( ) , 若f  x 在x0附近不变号 ( ) x0 则 f 不是极值.如下图： (极小值); 3. 极值的充分条件 极值的一阶充分条件 x y O x0    x y O x0    ( , ) . 0 o x0的某去心邻域U x  内可导

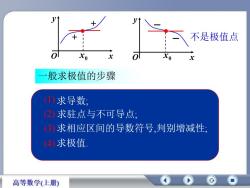
y不是极值点+1oXoxoxx般求极值的步骤(1)求导数;(2）求驻点与不可导点：(3)求相应区间的导数符号,判别增减性：(4)求极值高等数学（上册）

x0 x0     一般求极值的步骤 求导数; 求驻点与不可导点; 求相应区间的导数符号,判别增减性; 求极值. (1) (2) (3) (4) 不是极值点   x y O x y O

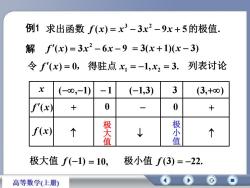
例1 求出函数 f(x)= x3-3x2-9x +5的极值.解 f'(x)= 3x2 -6x-9 = 3(x+1)(x-3)列表讨论令 f'(x)=0， 得驻点 xi =-1,x2 = 3. 死3x-1(-1,3)(-80,-1)(3,+8)00+f'(x)+极小值极大值+f(x)个个极大值 f(-1)=10,极小值 f(3)=-22.O高等数学（上册）

例1 解 ( ) 3 9 5 . 求出函数 f x  x 3  x 2  x  的极值 ( ) 3 6 9 2 f  x  x  x  令 f (x)  0， 1, 3. 得驻点 x1   x2  列表讨论 x (,1)  1 (1,3) 3 (3,) f (x) f (x)     0 0   极 大 值 极 小 值 极大值 f (1)  10, 极小值 f (3)  22.  3(x  1)(x  3)

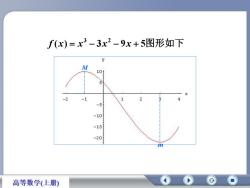
f(x)=x3-3x2-9x+5图形如下yM10521-2-1S-5-10-15-20m高等数学（上册）

( ) 3 9 5 3 2 f x  x  x  x  M m 图形如下

对于驻点，有时还可以利用函数在该点处的二阶导数的正负号来判断极值点极值的二阶充分条件定理3（第二充分条件）如果f'(x)= 0,f"(x) 0),则f(x)为极大值(极小值)高等数学（上册）

定理3(第二充分条件) ( ) 0, 如果 f  x0  极大值 (极小值). f (x0 )  0 ( 0),则f (x0 )为 极值的二阶充分条件 对于驻点,有时还可以利用函数在该点 处的二阶导数的正负号来判断极值点

例2求出函数f(x)=x3+3x2-24x-20的极值.解f(x) = 3x2 +6x - 24 = 3(x+ 4)(x-2)令 f'(x) = 0,得驻点 x = -4， x2 = 2.: f"(x) = 6x +6,：f"(-4)=-18 0,故极小值 f(2)=-48f(x)= x3 +3x2-24x-20 图形如下C高等数学（上册）

例2 解 ( ) 3 24 20 . 求出函数 f x  x 3  x 2  x  的极值 ( ) 3 6 24 2 f  x  x  x  令 f (x)  0， 4, 2. 得驻点 x1   x2   3(x  4)(x  2)  f ( x)  6x  6,  f (4)   18  0, 故极大值 f (4)  60, f (2)  18  0, 故极小值 f (2)  48. ( ) 3 24 20 3 2 f x  x  x  x  图形如下