《高等数学》课程教学资源（课件讲稿）第一章_1.4.1-1.4.2

第三节无穷小与无穷大一、无穷小二、无穷大三、小结思考题高等数学（上册）

一、无穷小 二、无穷大 三、小结 思考题 第三节 无穷小与无穷大

若limf(x)=0若limf(x）=0一、无穷小X-→x则f(x）是x→x。时的无穷小则f(x)是x→0时的无穷小l. 定义：如果函数 f(x)当x→x(或 x→)时的极限为零，那么称f(x)为当x→x(或x→8)时的无穷小：f(x)为当x→80时的无穷小f(x)为当x一→x时的无穷小台>0,3X>0,当x>X时，有000-8时，有f(x)<8f(x)|<8常用记号：α(x)、β(x)、(x)等高等数学（上册）

一、无穷小(infinitesimal) ) . ( ) ( ( ) ( ) 0 0 时的无穷小 时的极限为零 ，那么称 为当 或 如果函数 当 或       x f x x x 1. 定义: f x x x x 常 用 记 号 ：  ( x )、  ( x )、  ( x )等

1(-1)"limlimsin x =lim例如计算：x>0x→8 xn→>n:limsinx=0，：函数sin x是当x→O时的无穷小x->01=0，：函数二是当x→α时的无穷小limx>8xx(-1)"(-1)"=0，.数列是当n→8时的无穷小limn→00nn注意（1）无穷小是变量,不能与很小的数混淆：（2）零是可以作为无穷小的唯一的数高等数学（上册）

例如计算： 0 limsin 0, x x    函数sin x是当x  0时的无穷小. lim 0 , 1 x   x   1 x . x 函数 是当  时的无穷小 0 ( 1) lim , n n n   ( 1) { } . n n n 数列 是当 时的无穷小 注意（1）无穷小是变量,不能与很小的数混淆; （2）零是可以作为无穷小的唯一的数. 0 limsin x x   1 lim x   x  ( 1) lim n n n 

lim α(x) = 02.无穷小与函数极限的关系X→Xo定理1lim f(x)= A←> f(x)=A+α(x)X→Xo其中α(x)是当x→x.时的无穷小即：若limf（x）=A则f(x）=A+无穷小若f（x）=A+无穷小则limf（x）=A意义给出了函数f(x)在 x。附近的近似表达式 f(x)～ A,误差为α(x)高等数学（上册）

2. 无穷小与函数极限的关系: 0 0 lim ( ) ( ( ) ) ( ), x x f x A f x x A x x x         定 理 1 其 中 是 当 时 的 无 穷 小 . 意义 0 ( ) ( ) , ( ). f x x f x  A  x 给出了函数 在 附近的近似表达 式 误差为 0 lim ( ) 0 x x  x   即：

3.无穷小的运算性质：定理2在自变量的同一变化过程中，有限个无穷小的代数和仍是无穷小注意：无穷多个无穷小的代数和未必是无穷小例如，n→时，一是无穷小，但n个一之和为1不是无穷小n定理3有限个无穷小的乘积也是无穷小定理4有界函数与无穷小的乘积是无穷小推论常数与无穷小的乘积是无穷小1例如,当x→o时,xsin=xarctan- =福福xx11所以,当x→o时，xsin都是无穷小arctanxxx高等数学（上册）

1 2 1 , x 0 , x sin , x arctan x x 所以 当  时 都是无穷小 推论 常数与无穷小的乘积是无穷小. 定理3 有限个无穷小的乘积也是无穷小. 3. 无穷小的运算性质: 定理2 在自变量的同一变化过程中,有限个无穷小 的代数和仍是无穷小. 注意：无穷多个无穷小的代数和未必是无穷小. 例如 时 是无穷小， n n 1 ,   , 1 . 1 但 个 之和为 不是无穷小 n n 定理4 有界函数与无穷小的乘积是无穷小. 1 , x 0 , x sin x 例如 当  时  0 0

3.无穷小的运算性质：定理2在自变量的同一变化过程中，有限个无穷小的代数和仍是无穷小注意：无穷多个无穷小的代数和未必是无穷小例如，n→o时，一是无穷小，但n个一之和为1不是无穷小定理3有界函数与无穷小的乘积是无穷小推论1在自变量的同一变化过程中，有极限的变量与无穷小的乘积是无穷小推论2常数与无穷小的乘积是无穷小推论3有限个无穷小的乘积也是无穷小例如,当x→0时,xsin 都是无穷小一x-arctan-x高等数学（上册）

x x x x x 1 , arctan 1 , 0 , sin 例如 当  时 2 都是无穷小 推论1 在自变量的同一变化过程中,有极限的变量 与无穷小的乘积是无穷小. 推论2 常数与无穷小的乘积是无穷小. 推论3 有限个无穷小的乘积也是无穷小. 3. 无穷小的运算性质: 定理2 在自变量的同一变化过程中,有限个无穷小 的代数和仍是无穷小. 注意：无穷多个无穷小的代数和未必是无穷小. 例如 时 是无穷小， n n 1 ,   , 1 . 1 但 个 之和为 不是无穷小 n n 定理3 有界函数与无穷小的乘积是无穷小

二、无穷大(infinite)limf（x）=00的定义：M-S定义XX定义2设函数f(x)在x某一去心邻域内有定义（或x大于某一正数时有定义）．如果对于任意给定的正数M（不论它多么大），总存在正数（或正数X），使得对于适合不等式0X）的一切x,对应的函数值f(x)总满足不等式f(x）>M则称函数f(x）当x→x（或x→80)时为无穷大记作lim f(x) = 00(或 lim f(x) = 0)x-→xo店高等数学（上册）

二、无穷大(infinite) 绝对值无限增大的变量称为无穷大

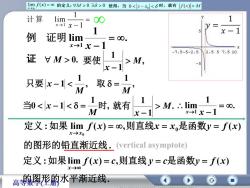
limf(x)=00的定义：M>038>0使得，当0M11计算lim8-→1x-11x-1例证明lim8x→1 x-1X7.55-2.52.557.510证VM>0. 要使MCx.1取8只要|x-1MM1二当0<x-1<=时，就有:.JimM.:8.Mx-1x -1x-定义:如果 lim f(x)= o0,则直线x = x,是函数y= f(x)x-→xo的图形的铅直渐近线.（verticalasymptote）定义:如果limf(x)=c,则直线y=c是函数y=f(x)X-高等的图形的水平渐近线

. 1 1 lim 1   x x  例 证明 证  M  0. , 1 1 M x   要使 , 1 1 M 只要 x   , 1 M 取   , 1 当0 1 时M  x     . 1 1 M x   就有 . 1 1 lim 1     x x . : lim ( ) , ( ) 0 0 的图形的铅直渐近线 定义 如果 f x 则直线x x 是函数y f x x x      (vertical asymptote) . : lim ( ) , ( ) 的图形的水平渐近线 定义 如果 f x c 则直线 y c是函数y f x x     (horizontal asymptote) 1 1 lim x x 1   计算 

特殊情形：正无穷大，负无穷大，(或 lim f(x)=-oo)lim f(x) = +ox-→xox-→xo(x-→8)(x→0)注意（1）无穷大是变量,不能与很大的数(如101000)混淆：(2)lim f(x)= 是没有极限的x-→>xo（3）无穷大一定无界,但无界函数不一定无穷大列如，当x→0时==sin高等数学（上册）

特殊情形：正无穷大，负无穷大． lim ( ) ( lim ( ) ) ( ) ( ) 0 0         f x f x x x x x x x 或 注意 1 1 , x 0 , y sin . x x 例如 当  时  （3）无穷大一定无界,但无界函数不一定无穷大. 0 (2) lim ( ) . x x f x   是没有极限的 （1）无穷大是变量,不能与很大的数(如 )混淆; 1000 10

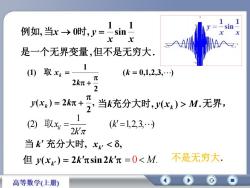
例如,当x→0时,y=二sinxx是一个无界变量，但不是无穷大。1(1) 取xk(k = 0,1,2,3,...)元2k元+2元y(xk) = 2k元 +当k充分大时,y(x)>M.无界，21(2)取xk(K =1,2,3,..)2k元当k充分大时，x<8,不是无穷大但 y(x)= 2k'元sin2k'元 =0<M.高等数学（上册）

, . 1 sin 1 , 0 , 是一个无界变量 但不是无穷大 例如 当 时 x x x  y  ( 0,1,2,3, ) 2 2 1 (1)       k k 取 xk , 2 ( ) 2  y xk  k  k , y(x ) M. 当 充分大时 k  1 (2) ( 1,2,3, ) 2 k x k k      取   ,  , 当 k 充分大时 xk 但 y( xk)  2ksin 2k  0  M. 不是无穷大． 无界