《线性代数》课程教学资源（课件讲稿，B）第五章二次型_5-1实二次型及其标准形

第五章S1实二次型及其标准形一、二次型及其矩阵表示二、二次型的标准形三、标准形的化法加油！

§1 实二次型及其标准形 第五章 一、二次型及其矩阵表示 二、二次型的标准形 三、标准形的化法

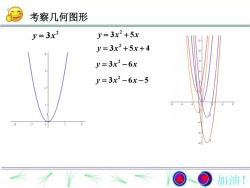
考察几何图形J = 3x?y = 3x? +5xy = 3x2 +5x+4y =3x? -6xy=3x2 -6x-5加油！

2 y x  3 2 y x x   3 5 2 y x x    3 5 4 考察几何图形 2 y x x   3 6 2 y x x    3 6 5

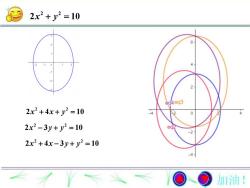
2x2 + y2 =10612eq4eq32x2 +4x+ y2 =100-4-2x2-3y+ y2=10eq2-22x2+4x-3y+ y2 =10加油！

2 2 2 10 x y   2 2 2 4 10 x x y    2 2 2 3 10 x y y    2 2 2 4 3 10 x x y y    

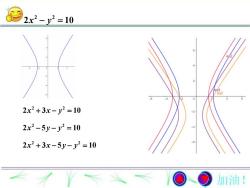
y2 = 100-R2x2+3x-y2=10-22x2-5y-y2=102x2 +3x-5y- y2=10加油！

2 2 2 3 10 x x y    2 2 2 5 10 x y y    2 2 2 3 5 10 x x y y     2 2 2 10 x y  

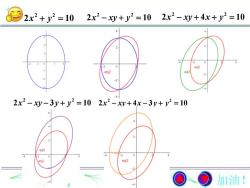
2x2 + y2 = 102x2 -xy + y =102x2 - xy+4x+ y2 =10-22eq2eq2eq322x2-xy-3y+y2=102x2-xy+4x-3y+y2=10eq3904-21eq2P加油！

2 2 2 10 x y   2 2 2 10 x xy y    2 2 2 4 10 x xy x y     2 2 2 3 10 x xy y y     2 2 2 4 3 10 x xy x y y     

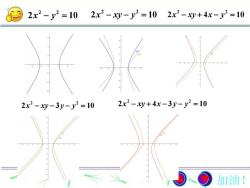
2x2 -xy- y2 = 102x2- xy+ 4x-y2 =102x2 - y2 =102x2-xy+4x-3y-y2=102x2-xy-3y- y=10加油！

2 2 2 10 x y   2 2 2 4 10 x xy x y     2 2 2 4 3 10 x xy x y y      2 2 2 10 x xy y    2 2 2 3 10 x xy y y    

一、二次型及其矩阵表示定义1n元二次齐次多项式f(x1,X2,..,xn)= ax +2ai2Xix + ..+2ainxix.+a22x? +...+2a2nX,xn-+...+annx'称为n元二次型，简称二次型x+xx,+3xx,+2x -4x,x,+3x当a,是实数时,f称为实二次型当a,是复数时,f称为复二次型ixx, -5x2 +(3+i)x2x, + /2xix加油！

  2 1 2 11 1 12 1 2 1 1 2 22 2 2 2 2 , , , 2 2 2 n . n n n n n nn n n f x x x a x a x x a x x a x a x x a x          定 元 义1 元二次齐 二次型， 次多项式 称为 简称二次型 , ij 当a f 是复数时 称为复二次型 一、二次型及其矩阵表示 2 2 2 1 1 2 1 3 2 2 3 3 x x x x x x x x x      3 2 4 3 2 1 2 2 2 3 1 4 ix x x i x x x x     5 (3 ) 2 , ij 当a f 是实数时 称为实二次型

二次型的矩阵表示1.取a;=aj，则2a,x,x, = a,x,x, +ajx,x,(i< j)于是 f =ax +a2xx, +..+anxxn+a21X,X + a2x2 +...+a2nX,xn+..+anx,Xi +an2X,X, +...+ann= xi(aui Xi + ai2X2 + ... + ainxXn)+ x2(a21Xi + a22X2 + ... + a2nXn)+...+ Xn(aniXi+ an2X2 +...+ annXn)加油！

二次型的矩阵表示 2 11 1 12 1 2 1 1 2 21 2 1 22 2 2 2 2 1 1 2 2 n n n n n n n n nn n f a x a x x a x x a x x a x a x x a x x a x x a x              ( ) ( ) ( ) 1 1 2 2 2 21 1 22 2 2 1 11 1 12 2 1 n n n nn n n n n n x a x a x a x x a x a x a x x a x a x a x                  2 ( ) ji ij ij i j ij i j ji j i 1 .取a a a x x a x x a x x i j     ，则 于是

aX+a++aa21Xi +a22x, +...+a2nx2n:1=[x,x2,..",xn]anix +an2x2 +.+annaua120x2a22(21a2n[xi,X2,...,xn]aan2nl加油！

11 12 1 1 21 22 2 2 1 2 1 2 [ , , , ] n n n n n nn n a a a x a a a x x x x a a a x                          11 1 12 2 1 21 1 22 2 2 1 2 1 1 2 2 [ , , , ] n n n n n n n nn n a x a x a x a x a x a x x x x a x a x a x                      

aua2Xaa21222n记A=anan2annX则二次型可记作f=XTAX.其中A称为二次型的矩阵显然，A是对称矩阵二次型与对称矩阵是一一对应加油！

11 12 1 1 21 22 2 2 1 2 , , n n n n nn n a a a x a a a x A X a a a x                           记 , . T 则二次型可记作 f X AX A  其中 称为二次型的矩阵 显然，A是对称矩阵. 二次型与对称矩阵是一一对应