《高等数学》课程教学资源（课件讲稿）第四章_4.2换元积分法

第二节换元积分法第一类换元法二、 第二类换元法三、 小结 思考题

第二节 换元积分法 • 一、第一类换元法 • 二、第二类换元法 • 三、小结 思考题

一、第一类换元法问题sin 2xdx ? -cos2x+C,利用复合函数，设置中间变量解决方法过程令t=2x=dx=dt.一21sin 2xdx=cos2x+Ccost+C二sin tdt =222

问题 sin 2xdx  = − + cos 2 , x C 解决方法 利用复合函数，设置中间变量. 过程 令 t = 2x , 2 1  dx = dt sin 2xdx  1 sin 2 = tdt  1 cos 2 = − +t C 1 cos 2 . 2 = − + x C 一、第一类换元法

在一般情况下：设 F'(u) = f(u), 则 [ f(u)du= F(u)+C.如果u=β(x）（可微）dF[p(x)] = f[p(x)lp'(x)dx[ f[0(x)]g'(x)dx = F[0(x)]+ C=If f(u)dul=8(x)由此可得换元法定理

在一般情况下： 设 F(u) = f (u), 则 ( ) ( ) .  f u du = F u + C 如果 u = (x) （可微）  dF[(x)] = f [ (x)](x)dx  = + f x x dx F x C [ ( )] ( ) [ ( )]      ( ) [ ( ) ] u x =  f u du = 由此可得换元法定理

定理1设f(u)具有原函数,u=(x)可导则有换元公式[ f[o(x)]p'(x)dx =J f(u)dulu=(x)第一类换元公式（凑微分法）说明：使用此公式的关键在于将[ g(x)dx化为[ f[o(x)lp(x)dx.观察重点不同，所得结论不同

( ) ( ) , ( ) [ ( )] ( ) [ ( ) ] u x f u u x f x x dx f u du     = =  =   设 具有原函数 可导， 则有换元公式 第一类换元公式（凑微分法） 说明:使用此公式的关键在于将 g x dx f x x dx ( ) [ ( )] ( ) .     化为 观察重点不同，所得结论不同. 定理1

一般地变形找f[p(x)lp'(x)dxg(x)dx凑微分式换元凑微分f[p(x)]dp(x)0(x)=u J f(u)du积分还原变量F[g(x)I+C.F(u)+C

一般地  g x( )dx   ====== [ ( )] ( )d f x x   x  ==== [ (  f x  )]d( ) x ====== ( )d f u u === ( ) + F u C ====== [ ( )]+ . F  x C 变形找 凑微分式 凑微分 换元 ( ) = x u 积分 还原变量

注:(l)定理说明：若已知f(u)du=F(u)+C则[ f[p(x)]lp'(x)dx = F[p(x)]+ C即[ f(u)du= F(u)+C中的u换成了另一个变量x的可微函数(x)后，式子仍然成立-又称为积分的形式不变性(2)由定理可见，虽然 [ f[p(x)]p'(x)dx是一个整体符号，但可把视为自变量微分—凑微分 Φ'(x)dx = dp(x)(3)凑微分法就在凑微分上，其基本思想就是对被积表达式进行变形，主要考虑如何变化(x)

注: (1) ( ) ( ) [ ( )] ( ) [ ( )] f u du F u C f x x dx F x C    = +  = +   定理说明：若已知 则 ( ) ( ) ( ) f u du F u C u x x  = + 即 中的 换成了另一个 变量 的可微函数 后,式子仍然成立 ——又称为积分的形式不变性 (2) [ ( )] ( ) ( ) ( ) f x x dx dx x dx d x       =  由定理可见，虽然 是一个整体符号，但可把 视为自变量微分 ——凑微分 (3)凑微分法就在凑微分上，其基本思想就是对 被积表达式进行变形，主要考虑如何变化f(x)

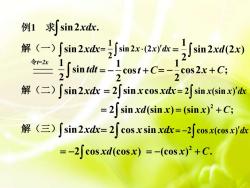
例1 求[ sin2xdx.1解（一）（sin2xdx=sin 2x·(2x)'dx :sin 2xd(2x)一-22令t=2x引二sin tdt = -=cos2x +C;cost+C=22解（二)[sin2xdx =2 sinxcosxdx=2[ sin x(sin x)'dx= 2J sin xd(sin x)= (sin x)° + C;解 (三) [ sin2xdx= 2[ cos x sin xdx=-2J cos x(cos x)'dx= -2[ cos xd(cosx) = -(cos x) + C

例1 求 sin2 .  xdx 解（一） sin2xdx  = sin2 (2 ) 2 1 xd x cos2 ; 2 1 = − x + C 解（二）  sin2xdx  = 2 sin xcos xdx = 2 sin (sin ) xd x  2 = + (sin ) ; x C 解（三）  sin2xdx= 2 cos sin x xdx   = −2 cos xd(cos x) 2 = − + (cos ) . x C 1 sin 2 tdt  令t=2x 1 cos 2 = − +t C 1 sin 2 (2 ) 2 =  x x dx   = 2 sin (sin ) x x dx   = −2 cos (cos ) x x dx  

求例2dx.3+2x111解(3 +2x),3+2x23+2x2rdx=d(3 +2x)-3+2x2/3+2xd=↓nu1+=↓m/3+2x+C.2J f(ax+b)dx==] f(u)dulu=ax+b一般地adx ==d(ax + b)a

例2 求 . 3 2 1 dx x  + 解 (3 2 ) , 3 2 1 2 1 3 2 1  +  + =  + x x x dx x  3 + 2 1 x dx x (3 2 ) 3 2 1 2 1  +  + =  du u  = 1 2 1 = ln | u | +C 2 1 ln | 3 2 | . 2 1 = + x +C  f (ax + b)dx =  u=ax+b f u du a [ ( ) ] 1 一般地 1 d d( ) x ax + b a = d(3 2 ) + x

例3.求[ (ax + b)" dx.解：当m±-1时令u=ax+b，则du=adx,故1 1原式=Jum-du_-m+1+Cuam+1a1(ax+ b)m+1 +Ca(m+1)当m=-1时dx-In|ax+b|+Cax+b

( ) d . m a x b x +  解: 令u a x b = + , 则 d d , u a x = 故 原式 = 1 d m u u a  1 1 1 1 m u C a m + =  + + 1 1 ( ) ( 1) m ax b C a m + = + + + 当m = −1时 d 1 ln x a x b C a x b a = + + +  当m  −1时 例3. 求

X例4dxS(2 + x)解令2+x=u则x=u-2 dx=du福r(u-2)2dx=du(2 + x)3ds= [(u- - 4u-* + 4u-du2C= In+uA24+C= In x + 2|+(x + 2)2x+2

例 4 2 3d (2 ) x x + x  解 令2 = + x u 则x u= 2 −2 3 ( 2) d u u u− =  2 4 2 ln 2 2 ( 2) x C x x = + + − + + + d d x u = 2 3d (2 ) x x + x  ( ) 1 2 3 u u u u 4 4 d − − − = − +  2 4 2 ln u C u u = + − +