《高等数学》课程教学资源（课件讲稿）第五章_5.1定积分的概念和性质

第五章定积分定积分和不定积分是积分学的两个主要组成部分.不定积分侧重于基本积分法的训练，而定积分则完整地体现了积分思想种认识问题、分析问题、解决问题的思想方法

第五章 定积分 定积分和不定积分是积分学的两个主要 组成部分.不定积分侧重于基本积分法的 训练,而定积分则完整地体现了积分思想 —一种认识问题、分析问题、解决问题的 思想方法

第一节定积分的概念和性质定积分问题举例二、定积分的定义三、 定积分的性质四、小结

第一节 定积分的概念和性质 • 一、定积分问题举例 • 二、定积分的定义 • 三、定积分的性质 • 四、小结

大图网DAIMG.CNO:2012050100005110

定积分问题举例实例1（求曲边梯形的面积）y= f(x)曲边梯形由连续曲线y= f(x)(f(x)≥0)A=?x轴与两条直线x=abaolxx=b所围成

a b x y o A = ? 实例1 （求曲边梯形的面积） y = f (x) 一、定积分问题举例 ( )( ( ) 0) . y f x f x x x a x b =  = = 曲边梯形由连续曲线 、 轴与两条直线 、 所围成

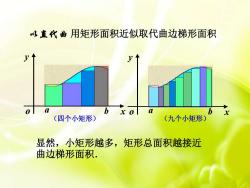
以直代曲用矩形面积近似取代曲边梯形面积6aahDX-X（四个小矩形）（九个小矩形）显然，小矩形越多，矩形总面积越接近曲边梯形面积

a b x y a b x o y o 以直代曲 用矩形面积近似取代曲边梯形面积 显然，小矩形越多，矩形总面积越接近 曲边梯形面积． （四个小矩形） （九个小矩形）

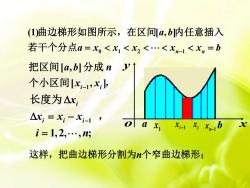
(1)曲边梯形如图所示，在区间[a,b内任意插入若干个分点a=x,<x, <x,< <xn-1<x,=b把区间[a,b]分成nJ个小区间[xi-1,x;],长度为△Ar;Ax, = X; - Xi-1 'olaxXi-1 X, x-,bi=1,2,.,n;这样，把曲边梯形分割为n个窄曲边梯形：

1 [ , ] [ , ] i i a b n x x − 把区间 分成 个小区间 ， a b x yo i x 1 x i 1 x − n 1 x − 这样，把曲边梯形分割为n个窄曲边梯形； 1 1,2, , ; i i i i x x x x i n −   = − = 长度为 ， 0 1 2 1 (1) [ , ] n n a b a x x x x x b =      = − 曲边梯形如图所示，在区间 内任意插入 若干个分点

(2)在每个小区间[x;-1,x;]上任取一点,以[xi-1,x;为底，f()为高的小矩形的面积近似窄曲边梯形的面积，则A, ~ f(E)Ax, i = 1,2,..,n(3)曲边梯形面积的近似值为ZAA, ~E f(5,)Ar;A=olbaXXn-1Xi-1i-1(4)当分割无限加细时,设所有小区间长度的最大值=max[△xj,△x2,…Ax,}，当→0时,Zf(5)Ax;曲边梯形面积为 A=lim1-0i=1

1 1 ( ) n n i i i i i A A f ξ x = = =      (3)曲边梯形面积的近似值为 1 2 (4) , max{ , , } 0 n λ =    → x x x λ 当分割无限加细时 设所有小区间长度的 最大值 ，当 时， i n i i A =  f x = → lim ( ) 1 0   曲边梯形面积为 1 (2) [ , ] i i i x x ξ 在每个小区间 − 上任取一点 ， ( ) 1,2, , A f i i i    = ξ x i n 1 [ , ] ( ) i i i x x f ξ 以 − 为底， 为高的小矩形的 面积近似窄曲边梯形的面积，则 a b y o i x 1 x i 1 x − n 1 x −  i

实例2（求变速直线运动的路程）设某物体作直线运动，已知速度v=v(t)是时间间隔[T,T]上t的一个连续函数，且v(t)≥0，求物体在这段时间内所经过的路程思路：以不变代变 把整段时间分割成若干小段，每小段上速度看作不变，求出各小段的路程再相加，便得到路程的近似值，最后通过对时间的无限细分过程求得路程的精确值

实例2 （求变速直线运动的路程） 设某物体作直线运动，已知速度v = v(t)是 时间间隔[ , ] T1 T2 上 t 的一个连续函数，且 v(t)  0，求物体在这段时间内所经过的路程. 思路：以不变代变 把整段时间分割成若干小段， 每小段上速度看作不变，求出各小段的路程再 相加，便得到路程的近似值，最后通过对时间 的无限细分过程求得路程的精确值．

T=t <ti<t,<...<tn-i<tn =T(1)分割At, = t; -ti-1(2)近似4S, ~v(t,)At, i =1,2,..,n则 S~Zv(t,)At;(3)求和i=1(4)取极限a = max[Ati,At2,...,△tn}2路程的精确值v(T,)At;S=lim1-0i-l

(1)分割 1 0 1 2 1 T2 T t t t t t =  n−  n =  i = i − i−1 t t t ( ) 1,2, , (2)近似    S v t i n i i i  = 1 ( ) n i i i S v t   = 则   (4)取极限 max{ , , , } 1 2 n  = t t  t 0 1 lim ( ) n i i i S v t    → = 路程的精确值 =  (3)求和

二、定积分的定义定义设函数f(x)在[a,b]上有界,在[a,b中任意插入若干个分点a= x<x <x,<…<xn-<x,=b把区间[a,b]分成n个小区间[x;-1,x;l(i=1,2,,n),各个小区间的长度为△x, = x; -xi-i(i=1,2,…),在每个小区间上任取一点5;(x;-1 ≤5,≤ x,),作乘积f(5:)△x;Zf(5,)Ax,(i=1,2,.),并作和S =i-1记a=max[△xj,Ar,,…,Ar,},如果不论对[a,b]怎样的

定义 0 1 2 1 1 1 1 1 ( ) [ , ] , [ , ] [ , ] [ , ]( 1,2, , ), ( 1,2, ), ( ), ( ) ( 1,2, ), ( ) , max{ n n i i i i i i i i i i i n i i i f x a b a b a x x x x x b a b n x x i n x x x i x x f x i S f x x      − − − − = =      = =  = − =    = =  =   设函数 在 上有界 在 中任意插入 若干个分点 把区间 成 个小区间 各个小区间的长度为 在每 个小区间上任取一点 作乘积 并作和 记 1 2 , , , }, [ , ] n   x x a b 如果不论对 怎样的 二、定积分的定义