《高等数学》课程教学资源（matlab及案例）2Matlab数值运算

实验2数值运算MATLAB

实验2 MATLAB 数值运算

实验目的和内容实验目的了解MATLAB中矩阵和多项式的创建，以及数值函数的建立。掌握矩阵运算，多项式运算、数值函数的运算。实验内容首先介绍MATLAB中矩阵的创建，矩阵的运算：其次介绍多项式的创建，多项式的四则运算，多项式求导、求根、求值等运算；最后介绍数值函数的建立，数值函数求值、求零点、求最大最小值、求定积分，数值函数作图等

实验目的和内容 实验目的 了解MATLAB中矩阵和多项式的创建，以及数值 函数的建立。掌握矩阵运算，多项式运算、数值函 数的运算。 实验内容 首先介绍MATLAB中矩阵的创建，矩阵的运算； 其次介绍多项式的创建，多项式的四则运算，多项 式求导、求根、求值等运算；最后介绍数值函数的 建立，数值函数求值、求零点、求最大最小值、求 定积分，数值函数作图等

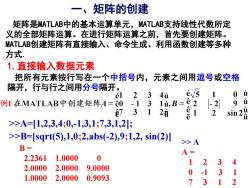
一、矩阵的创建矩阵是MATLAB中的基本运算单元，MATLAB支持线性代数所定义的全部矩阵运算。在进行矩阵运算之前，首先要创建矩阵。MATLAB创建矩阵有直接输入、命令生成、利用函数创建等多种方式.1.直接输入数据元素把所有元素按行写在一个中括号内，元素之间用逗号或空格隔开，行与行之间用分号隔开。ev5u1023é14u>A=[1,2,3,4;0,-1,3,1;7,3,1,2];>>B=[sqrt(5),1,0;2,abs(-2),9;1,2, sin(2)]>> AB=02.23611.0000329.00002.00002.000003-11.00002.00000.90932371

一、矩阵的创建 矩阵是MATLAB中的基本运算单元，MATLAB支持线性代数所定 义的全部矩阵运算。在进行矩阵运算之前，首先要创建矩阵。 MATLAB创建矩阵有直接输入、命令生成、利用函数创建等多种 方式. 1.直接输入数据元素 把所有元素按行写在一个中括号内，元素之间用逗号或空格 隔开，行与行之间用分号隔开。 >>A=[1,2,3,4;0,-1,3,1;7,3,1,2]; >> A A =      1     2     3     4      0    -1     3     1      7     3     1     2 >>B=[sqrt(5),1,0;2,abs(-2),9;1,2, sin(2)] B =     2.2361    1.0000         0     2.0000    2.0000    9.0000     1.0000    2.0000    0.9093

例2查看例1矩阵A中第2行第3列的元素，并将其修改为-3乘以原来的数。>>A(2,3)ans =30>> A(2,3)=(-3)*A(2,3)723A?132

例2 查看例1矩阵A中第2行第3列的元素，并将其修改 为-3乘以原来的数。 >> A A =      1     2     3     4      0    -1     3     1      7     3     1     2 >>A(2,3) ans = 3 >> A(2,3)=(-3)*A(2,3) A=      1     2     3     4      0    -1    -9     1      7     3     1     2

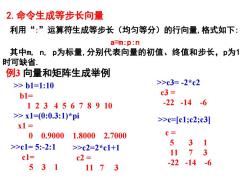
2.命令生成等步长向量利用“：”运算符生成等步长（均匀等分）的行向量，格式如下：a=m:p:n其中m，n，p为标量，分别代表向量的初值、终值和步长，p为1时可缺省例3向量和矩阵生成举例>>c3= -2*c2>> b1=1:10c3 =b1=-22 -14-612345678910>> x1=(0:0.3:1)*pi>>c=[c1;c2;c3]x1 =c=00.90001.80002.7000531>>c1= 5:-2:1>>c2=2*c1+13711c1=c2 =-22-14-653111 73

2.命令生成等步长向量 利用“:”运算符生成等步长（均匀等分）的行向量,格式如下: a=m:p:n 其中m, n, p为标量,分别代表向量的初值、终值和步长，p为1 时可缺省. 例3 向量和矩阵生成举例 >> b1=1:10   b1= 1  2  3   4  5  6  7  8  9  10 >> x1=(0:0.3:1)*pi    x1 =   0    0.9000    1.8000    2.7000 >>c1= 5:-2:1 c1= 5    3    1  >>c2=2*c1+1 c2 =       11   7     3    >>c3= -2*c2 c3 =    -22   -14    -6 >>c=[c1;c2;c3]  c =     5       3     1     11     7     3    -22   -14    -6

冒号的作用A（i，：）表示矩阵A的第i行所有元素组成的行向量，A（：，i)表示矩阵A的第i列所有元素组成的列向量。若B是向量，则B（i：j）表示B中分量i至分量j构成的新向量；若B是一个矩阵，则B（i：i)表示将B按列依次排列构成的向量的第i个分量至第j个分量。例4将向量b=[1,347-26]中的第2至第5个分量取出构造一个新的向量v>> b=[1,3 4 7 -2 6]>>v=b(2:5)V=347-2

冒号的作用 A(i,:)表示矩阵A的第i行所有元素组成的行向量， A(:,j)表示矩阵A的第j列所有元素组成的列向量。 若B是向量,则B(i:j)表示B中分量i至分量j构成的新向量； 若B是一个矩阵，则B(i:j)表示将B按列依次排列构成的向量的 第i个分量至第j个分量。 例4 将向量b=[1,3 4 7 -2 6]中的第2至第5个分量取出构造 一个新的向量v. >> b=[1,3 4 7 -2 6] >>v=b(2:5)      v=                3  4  7   -2

例5请输入一个3行3列的矩阵a，将a的第1行至第2行，第2列至第3列的元素组成的矩阵赋值给a1；将a的第1行至第2行构成的子矩阵赋值给a2：将a的第2列至第3列构成的子矩阵赋值给a3：将a的第1列元素构成的子矩阵赋值给a4：将a的第2行元素构成的子矩阵赋值给a5.>> a4=a(: ,1)>> a2=a(1:2, : )>>a=[1 2 3;4 5 6;7 8 9]a4 =a2 =a=123324656５7789>>a3= a( : ,2:3>> a1=a(1:2,2:3)a3 =>>a5= a(2 ,:)23al=a5 =5632569856

例5 请输入一个3行3列的矩阵a，将a的第1行至第2 行，第2列至第3列的元素组成的矩阵赋值给a1; 将 a 的第1行至第2行构成的子矩阵赋值给a2; 将a的第2列 至第3列构成的子矩阵赋值给a3; 将a的第1列元素构成 的子矩阵赋值给a4; 将a的第2 行元素构成的子矩阵赋 值给a5. >>a=[1 2 3;4 5 6;7 8 9] a1=      2     3      5     6 >> a2=a(1:2, : ) a2 =      1   2    3      4   5    6 >>a3= a( : ,2:3 a3 =      2     3      5     6      8     9 >> a4=a( : ,1) a4 =        1        4        7 >>a5= a( 2 ,:) a5 = 4     5     6 >> a1=a(1:2,2:3)  a=      1   2    3      4   5    6      7   8    9

3.利用内部函数产生矩阵利用MATLAB内部函数，可以产生一些常用的特殊矩阵义含函数名[]空矩阵eye (n)n阶单位矩阵元素全部为1的m×n矩阵ones (m, n)元素服从0到1之间均匀分布的m×n随机矩阵rand(m, n)元素服从零均值单位方差正态分布的m×n随机矩阵randn (m, n)元素全部为0的m×n矩阵zeros (m, n)n阶魔方矩阵magic(n)linspace（a,b，将[a,b]进行n-1等分，返回由端点及分段点坐标所产生的n个元素的n)行向量.当n缺省时，默认n=100例6随机产生一个3阶矩阵A，并计算2A+5I（其中I为单位矩阵）ans =>> A=rand(3);6.62941.82680.5570>> 2*A+5*eye(3)1.81166.26471.09380.25400.19516.9150

3. 利用内部函数产生矩阵 利用MATLAB内部函数，可以产生一些常用的特殊矩阵. 函数名 含 义 [ ] 空矩阵 eye(n) n阶单位矩阵 ones(m,n) 元素全部为1的m×n矩阵 rand(m,n) 元素服从0到1之间均匀分布的m×n随机矩阵 randn(m,n) 元素服从零均值单位方差正态分布的m×n随机矩阵 zeros(m,n) 元素全部为0的m×n矩阵 magic(n) n阶魔方矩阵 linspace(a,b, n) 将[a,b]进行 n-1等分，返回由端点及分段点坐标所产生的n个元素的 行向量.当n缺省时,默认n=100. 例6 随机产生一个3阶矩阵A，并计算2A+5I（其中I为单位矩阵） >> A=rand(3); >> 2*A+5*eye(3) ans =       6.6294    1.8268    0.5570      1.8116    6.2647    1.0938      0.2540    0.1951    6.9150

例7将区间[0,11进行5等分,写出等分点的坐标构成的向量，并将其中的1,2,5分量取出构成向量y>> x=linspace(0,1,6)x=00.20000.40000.60000.80001.0000>> y=x([1,2,5]J=00.80000.2000>> magic(3)例8生成特殊短陷6ans = 8>> ones(2,3)735ans =294111eye(3)>V111001ans=VVz[];001z(1)>>001索引超出数组范图

例7 将区间[0,1]进行5等分,写出等分点的坐标构成的向量， 并将其中的1,2,5分量取出构成向量y. >> x=linspace(0,1,6) x = 0 0.2000 0.4000 0.6000 0.8000 1.0000 >> y=x([1,2,5]) y = 0 0.2000 0.8000 例8 生成特殊矩阵 >>  ones(2,3)    ans = 1 1 1 1 1 1 >>  magic(3)            ans = 8 1 6 3 5 7 4 9 2 >>  eye(3)            ans = 1 0 0 0 1 0 0 0 1 >>  z=[];   >>  z(1)            索引超出数组范围

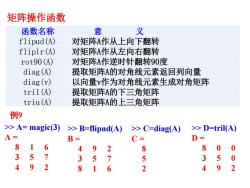
矩阵操作函数义意函数名称flipud(A)对矩阵A作从上向下翻转对矩阵A作从左向右翻转fliplr(A)rot90(A)对矩阵A作逆时针翻转90度diag (A)提取矩阵A的对角线元素返回列向量diag(v)以向量v作为对角线元素生成对角矩阵tril(A)提取矩阵A的下三角矩阵triu(A)提取矩阵A的上三角矩阵例9>> A= magic(3)>> D=tril(A)>> B=flipud(A)>> C=diag(A)A=D=B=C=861800849235735053579249282641

矩阵操作函数 函数名称 意 义 flipud(A) 对矩阵A作从上向下翻转 fliplr(A) 对矩阵A作从左向右翻转 rot90(A) 对矩阵A作逆时针翻转90度 diag(A) 提取矩阵A的对角线元素返回列向量 diag(v) 以向量v作为对角线元素生成对角矩阵 tril(A) 提取矩阵A的下三角矩阵 triu(A) 提取矩阵A的上三角矩阵 >> A= magic(3) A =      8     1     6      3     5     7      4     9     2 >> B=flipud(A) B =      4     9     2      3     5     7      8     1     6 >> C=diag(A) C =      8      5      2 >> D=tril(A) D =      8     0     0      3     5     0      4     9     2 例9