《高等数学》课程教学资源（matlab及案例）6非线性方程求根

实验6开普勒方程近似解与方程求根1.方程求根的Matlab指令2.“二分法”3.“牛顿切线法”4.一般迭代法5.MATLAB求方程组的近似解

1. 方程求根的Matlab指令 2. “二分法” 3. “牛顿切线法” 4. 一般迭代法 5. MATLAB求方程组的近似解 实验6 开普勒方程近似解 与方程求根

实验问题：求开普勒方程x=0.5sinx+1近似解分析：该问题可以转化为下列方程求根x- 0.5sinx- 1=0显然该方程为一元非线性方程，没有现成的求解公式6.1利用MATLAB命令求方程的近似根f=@(x)x-0.5*sin(x)-1;输出：c=1.4987c=fzero(f,[0,2])求f在区间[a,b的零点c=fzero(f,[a,b)求f在x.附近的零点c=fzero(f,xo)

实验问题: 分析：该问题可以转化为下列方程求根. 求开普勒方程 近似解. f=@(x)x-0.5*sin(x)-1; c=fzero(f,[0,2]) 6.1 利用MATLAB命令求方程的近似根 输出：c = 1.4987 显然该方程为一元非线性方程，没有现成的求解公式. c=fzero(f,[a,b]) 求f在区间[a,b]的零点 c=fzero(f,x0 ) 求f在x0附近的零点

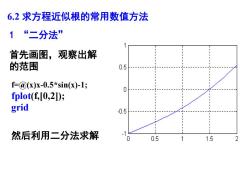
6.2求方程近似根的常用数值方法“二分法”首先画图，观察出解的范围0.5f=@(x)x-0.5*sin(x)-1;0fplot(f,[0,2D);grid-0.5然后利用二分法求解00.511.52

1 “二分法” f=@(x)x-0.5*sin(x)-1; fplot(f,[0,2]); grid 首先画图，观察出解 的范围 然后利用二分法求解 6.2 求方程近似根的常用数值方法

条件：f(a)f(b)0，f(x)连续且有唯一零点分析：t y[a,b]中点x, P[x,b]a=xβ[a,b]=[xj,b]aX, X30bX2[a,b]中点x, P [a,x,]xb=x, [a,b]=[xi,x,][a,b]中点x, [x3,x2]a=l[a,b]=[x3,x2]M得到第n个区间[a,b]中点x

分析： 条件： 得到第n个区间

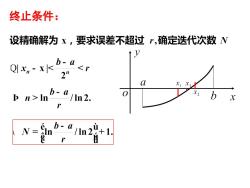
终止条件：设精确解为x，要求误差不超过r.确定迭代次数NVb-a42"aXX3b-aX20bx/ In 2.Dn >lnrb-eN+1nInee8

终止条件：

二分法求根程序：clear;f=@(x)x-0.5*sin(x)-1;a=0;b=1;r=1.0e-5;N=log((b-a)/r)/log(2); k=0;while n< =fix(N)+1k=k+1;c=(a+b)/2:if abs(f(c)==0break;elseif f(c)*f(b)<0a=c;elseb=c;endfprintf(k=%d, x=%.5fln',k,c);end

clear; f=@(x)x-0.5*sin(x)-1; a=0;b=1;r=1.0e-5; N=log((b-a)/r)/log(2); k=0; while n< =fix(N)+1 k=k+1;c=(a+b)/2; if abs(f(c))==0 break; elseif f(c)*f(b)<0 a=c; else b=c; end fprintf('k=%d, x=%.5f\n',k,c); end 二分法求根程序：

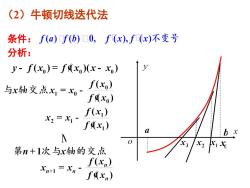
(2)牛顿切线迭代法条件：f(a)f(b)0,f(x),f(x)不变号分析：y- f(x)= fdx)(x- x)Lf(xo)与x轴交点x,=x。fdxo)f(x)x2 =xfdx)abxN0X2X3xX第n+1次与x轴的交点f(xn)Xn+1=x.fdxn)

（2）牛顿切线迭代法 分析： 条件：

生顿切线法收敛性定理：设f(x)在[a,b]上有二阶导数，且满足(1) f(a) ×f(b) < 0 ;(2)fx),f效x)在[a,b]上连续且不变号;则当初值x1[a,b]且f(x)与fx)同号时切线迭代法得到的迭代序列收敛于方程f（x）=0在[a,bl上的唯一实根

牛顿切线法收敛性定理：

程序：clear;m=min(abs(df(a),abs(df(b);f=@(x) x-0.5*sin(x)-1;k=0;df =@(x) 1-0.5*cos(x);while abs(f(x0)>m*dltd2f =@(x) 0.5*sin(x);k=k+1;a=1;b=2;dlt=1.0e-5;x1=x0-f(x0)/df(x0);if f(a)*d2f(a)>0x0=x1;x0=a;fprintf(k=%d x=%.5fln',k,x0)elseendx0=b;end运行结果：k=1x=1.54858k=2x=1.49933

clear; f=@(x) x-0.5*sin(x)-1; df =@(x) 1-0.5*cos(x); d2f =@(x) 0.5*sin(x); a=1;b=2;dlt=1.0e-5; if f(a)*d2f(a)>0 x0=a; else x0=b; end m=min(abs(df(a)),abs(df(b))); k=0; while abs(f(x0))>m*dlt k=k+1; x1=x0-f(x0)/df(x0); x0=x1; fprintf('k=%d x=%.5f\n',k,x0); end 程序： 运行结果： k=1 x=1.54858 k=2 x=1.49933 k=3 x=1.49870

(3)一般选代法Uf(x)= 0x= f(x)+x即x = g(x)取xo选代初值p xj =g(xo)p x,=g(x)N迭代格式p Xk+1 = g(x)NP (x k = 0,1,2,L迭代序列g(x) —迭代函数

（3） 一般迭代法 ——迭代格式 ——迭代序列 ——迭代初值 ——迭代函数