《高等数学》课程教学资源（课件讲稿）第二章_2.4函数的微分

第四节函数的微分01微分的概念02微分的几何意义03微分的计算04微分的应用

01 微分的概念 02 微分的几何意义 03 微分的计算 04 微分的应用 第四节 函数的微分

OA问题引入实例正方形金属薄片受热后面积的改变量（x)设边长由x.变到x。xXorar口正方形面积Ax, A (x x)x)AOxiXu2x。x (x)(1)(2)(1)：x的线性函数,且为A的主要部分;(2) :

问题引入 2 实例 正方形金属薄片受热后面积的改变量

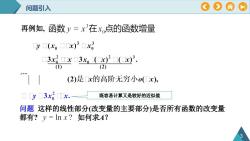
OOAA问题引入再例如，函数y=x在x.点的函数增量y(x。x) x)3xx3，x)(x)(1)(2)(2)是x的高阶无穷小o(x), y 3x, x.既容易计算又是较好的近似值问题这样的线性部分(改变量的主要部分)是否所有函数的改变量都有？=lnx？如何求A?

问题引入 3 再例如, 既容易计算又是较好的近似值 问题 这样的线性部分(改变量的主要部分)是否所有函数的改变量 都有? 如何求A？

OOAA微分的概念定义2.4设函数y=f(x)在x的某邻域U(x）内有定义，x。+DxiU(x。），(2.4)若函数增量Dy=f(x+Dx)-f(x）可表示为Dy= ADx + o(Dx)其中A是不依赖于Dx的常数，而o(Dx）是比Dx高阶的无穷小，那么称函数y=f(x)在点x.是可微的.而ADx叫做函数y=f(x）在点x，相应于自变量增量Dx的微分，记作dy|x，即：dyx-=ADx.1）ADx：称为Dy的线性主部，即dy注2Dx很小时，Dy》dy若Dy=ADx+o(Dx），则称dy=ADx为函数的微分

一、 微分的概念 4 定义2.4 注

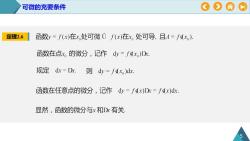
0O#0可微的充要条件定理2.6函数y=f(x)在x.处可微Uf(x)在x。处可导，且A=fdx）函数在点x。的微分，记作dy=fdx)Dx规定 dx=Dx则 dy=fdxo)dx.函数在任意点的微分，记作dy=fdx)Dx=fdx)dx显然，函数的微分与x和Dx有关5

可微的充要条件 5 定理2.6

OOA0微分的概念6求函数当口日0.02时的微分Ax解:(InOxAx0.02x=e4x=0.02x=e4x=0.02xe通常把自变量的增量称为自变量的微分，记作口即日年0四口即函数的微分与自变量的微分之商等于该函数的导数，导数也叫"微商”F

6 求函数 ᵮ= ᵮᵮ当ᵮ= ᵮ,  ᵮ= 0.02时的微分. ∵ ᵮᵮ= (lnᵮ) ′ᵮ 通常把自变量ᵮ的增量ᵮ称为自变量的微分, 记作ᵮᵮ,   即ᵮᵮ= ᵮ. ∴ ᵮᵮ= ᵮ′(ᵮ)ᵮᵮ. ᵮᵮ ᵮᵮ = ᵮ′(ᵮ). 即函数的微分ᵮᵮ与自变量的微分ᵮᵮ之商等于该函数的导数.  导数也叫"微商". 例 1 解 一、 微分的概念

OOA例求函数In/x?+y2=arctan的微分dy.xV解原式等价于-In(x? + v2= arctan2x12x +2yyexve-1xve-两边对x求导得h2ayoXX1+Sxox+y即x+yy=xy-y，化简整理得y=x-yx+ydx所以dy店x-1

7 例 2 解

第四节函数的微分微分的概念0102微分的几何意义03微分的计算04微分的应用

微分的概念 微分的几何意义 03 微分的计算 01 04 微分的应用 02 第四节 函数的微分

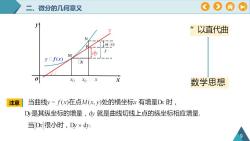
OOA二、微分的几何意义yt以直代曲N1o(x)JdyMJf(x)Dx0xxoxxo数学思想当曲线y=f(x)在点M(xy)处的横坐标x有增量Dx时注意Dy是其纵坐标的增量，dy就是曲线切线上点的纵坐标相应增量当Dx很小时，Dy》dy9

二、微分的几何意义 9 注意 M N T ） P

0O?二、微分的几何意义当Dx充分小，fdx）1O时，函数y=f(x）的改变量Dy与微分dy的关系是(D）例A. Dy = dyB. Dy dyD. Dy 》 dy若f(x)可微，当Dx0时，在点x处的Dy-dy是关于Dx的（A）C.同阶无穷小A.高阶无穷小B.等价无穷小D.低阶无穷小

二、微分的几何意义 10 例 3 例 4 D A