《线性代数》课程教学资源(课件讲稿,C)第四章 4-3非齐次线性方程组

第四章线性方程组第三节非齐次线性方程组
第四章 线性方程组 第三节 非齐次线性方程组

第四章线性方程组一、非齐次线性方程组解的性质aiXi +ai2x, +... +ainxn = b,a21x +a22x2 +...+a2nxn =b2Ax = bb+axamiX +am2X +.nmbauXiazinb2X2(2)a22a2n记A:.b,x=一b01n2mmn
第四章 线性方程组 一、非齐次线性方程组解的性质 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 11 12 1 1 1 21 22 2 2 2 1 2 , . , , n n n n m m mn n m n n n n mn n m a x a x a x b a x a x a x b a x a x a x b a a a x b a a a x b A x b a a a x b , 记

第四章线性方程组aixi +a2x +...+ainx, = 0,a21Xi +a22X2 +... +a2nx, =0,Ax=0.amiX, +am2X, +...+amnx, = 0.该方程组称为对应的齐次线性方程组
第四章 线性方程组 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0, 0 0. n n n n m m mn n a x a x a x a x a x a x a x a x a x , Ax=0. 该方程组称为对应的齐次线性方程组

第四章线性方程组性质1 设x=n,及x =n,是方程组 Ax=b的解则x=n -n,是其对应的齐次方程组Ax=0的解证明: Ani=b, Anz = b:. A(n - nz) = b - b = 0.即x= ni-n2满足方程Ax = 0
第四章 线性方程组 1 2 1 2 . 1 0 x x Ax b x Ax 设 及 是方程组 的解, 则 是其对应的齐次方程组 性 的解 质 证明 0. A 1 2 b b 0. 即x 1 2满足方程Ax A1 b, A2 b

第四章线性方程组性质2设x=n是方程组Ax=b的解,x=ε是方程组Ax=0的解,则x=n+E是方程组Ax=b的解证明A(+n)= A+An=0+b=b,所以x=+n是方程Ax=b的解
第四章 线性方程组 0 2 x Ax b x Ax x Ax b 设 是方程组 的解, 是方程组 的解,则 是方程组 性质 的解 证明 A A A 0 b b, 所以x 是方程 Ax b的解

第四章线性方程组二、非齐次线性方程组的通解x =k5i +k,5, +...+kn-r+nn其中 5i,52,……,亏n-r是对应齐次方程组的基础解系kj,kz,...,kn-r为任意实数m*是非齐次方程组的特解
第四章 线性方程组 二、非齐次线性方程组的通解 * 1 1 2 2 n r n r x k k k 1 2 , , , n r k k k 1 2 , , , n r 其中 是对应齐次方程组的基础解系, 为任意实数

第四章线性方程组例1:求解方程组X+x-3x-x=1 3x, -x, -3x + 4x = 4Xi +5x, -9x, -8x =0解:对增广矩阵进行初等行变换化成行最简形1 1 -3 -1 1r,-3rl1113A=|3 -1 3414-6-7 -1-9-80
第四章 线性方程组 1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x 例1:求解方程组 1 1 3 1 1 3 1 3 4 4 1 5 9 8 0 A 2 1 3 1 3 1 1 3 1 1 ~ 0 4 6 7 1 0 4 6 7 1 r r r r 解: 对增广矩阵进行初等行变换化成行最简形

第四章线性方程组3351-31-213r-r324400000于是得与原方程组同解的方程组335X +x -3x-x =1,xiX243x-x2-3xg +4x =437Xi +5x2 -9x3 -8x4 = 0X24
第四章 线性方程组 3 2 2 1 1 3 1 1 3 7 1 ~ 0 1 244 1 ( ) 0 0 0 0 0 4 r r r 1 2 3 3 5 1 0 2 4 4 3 7 1 ~ 0 1 244 0 0 0 0 0 r r 于是得与原方程组同解的方程组 1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 , 2 4 4 x x x x x x 1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x
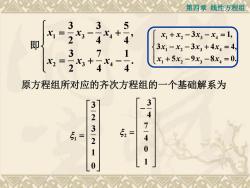
第四章线性方程组33XiX3X +x,-3x-x=1,-27即3x, -X, -3x, +4x = 4,3X, +5x, -9x, -8x =0X2C2原方程组所对应的齐次方程组的一个基础解系为331247315141201
第四章 线性方程组 1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 . 2 4 4 x x x x x x 即 原方程组所对应的齐次方程组的一个基础解系为 1 3 2 3 2 1 0 2 3 4 7 4 0 1 1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x

第四章线性方程组5取 x,= x4=0 的原方程组的一个特解41=-40-因此,原方程组的通解为33512XI4AX +x, -3x -x4 =1,3-27X2+kz=k+143x-x2-3x +4x =4专100x+5x,-9x,-8x4=0X4]0其中k,k,为任意数
第四章 线性方程组 取 3 4 x x 0 的原方程组的一个特解 * 5 4 1 4 0 0 1 2 1 2 3 4 3 3 5 2 4 4 3 7 1 2 4 4 1 0 0 0 1 0 x x k k x x 因此,原方程组的通解为 其中k1 ,k2为任意数 1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-2齐次线性方程组.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-1线性方程组有解的判定.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-3向量组的线性关系.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-2向量及其线性运算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-1消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-4分块矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-3初等矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-2逆矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-1矩阵的运算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-4矩阵的秩.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-4克拉默法则.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-3行列式的计算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-2行列式的性质.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-1n阶行列式的概念.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第二章行列式_第五节 矩阵的秩.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第一章矩阵及其初等变换_第二节 高斯消元法与矩阵的初等变换.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第一章矩阵及其初等变换_第一节 矩阵及其运算.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第四节 实对称矩阵的相似对角化_4.4 实对称矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第二节 矩阵的相似对角化_4.2 矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第三节 n维向量空间的正交性_4.3 n维向量空间的正交性.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-九年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-九年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-七年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-七年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-八年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-八年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-六年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-六年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_学生用书(不全)必修3.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_学生用书(不全)必修4.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_教师用书(不全)必修2.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_教师用书(不全)必修3.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_教师用书(不全)必修4.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_学生用书(不全)必修2.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章_0 高等数学简介.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章_1.1 函数.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章_1.2极限的概念与性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章_1.3 极限的运算法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章_1.4 无穷小与无穷大.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章_1.5函数的连续性.pdf
