《线性代数》课程教学资源（课件讲稿，C）第二章 2-4矩阵的秩

第二章矩阵与向量第四节矩阵的秩

第二章 矩阵与向量 第四节 矩阵的秩

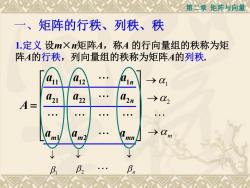
第二章矩阵与向量一、矩阵的行秩、列秩、秩1.定义设mXn矩阵A，称A的行向量组的秩称为矩阵A的行秩，列向量组的秩称为矩阵A的列秩W→αInaa221→α22n21A=→α00mmlm2mnβ,βB1

第二章 矩阵与向量 1.定义 设m×n矩阵A，称A 的行向量组的秩称为矩 阵A的行秩，列向量组的秩称为矩阵A的列秩. 一、矩阵的行秩、列秩、秩 11 12 1 21 22 2 1 2 n n m m mn a a a a a a A a a a              1 2  m 1   2   n 

第二章矩阵与向量0例1设矩阵A=12，求它的行秩和列秩2解： A的行向量α, =(1,0,1),α, =(0,1,2),α, =(2,1,4)0由行列式012=0，知向量组α,α,α,线性相关，21又α,α,线性无关，故α,α,是A的行向量组的一个最大无关组，所以矩阵A的行秩等于2

第二章 矩阵与向量 1 0 1 1 0 1 2 2 1 4 A            例 设矩阵 ，求它的行秩和列秩 1 2 3 A的行向量      (1,0,1), (0,1,2), (2,1,4) 1 2 3 1 0 1 0 1 2 0 , , 2 1 4 由行列式  ，知向量组   线性相关， 解： 1 2 1 2 , , 2. A A 又    线性无关，故 是 的行向量组的一个 最大无关组，所以矩阵 的行秩等于

第二章矩阵与向量3111例2 求矩阵A=2的行秩和列秩01000解：A的行向量α, =(1,1,3,1),α, =(0,2,-1,4),α, = (0,0, 0,5)去掉第三个分量的α, =(1,1,1),α, =(0,2,4),α, =(0,0,5)L由行列式0=10±0，知向量组α,α,α线性无关21500所以A的行秩为3向量组α,αz,α,也线性无关

第二章 矩阵与向量 1 2 3 A的行向量       (1,1,3,1), (0,2, 1,4), (0,0,0,5) 1 1 3 1 2 0 2 1 4 0 0 0 5 A             例 求矩阵 的行秩和列秩 解： 1 2 3 去掉第三个分量的         (1,1,1), (0,2,4), (0,0,5) 1 2 3 111 0 2 4 10 0 , , 005 由行列式   ，知向量组     线性无关. 1 2 3 向量组   , , 也线性无关 所以A的行秩为3

第二章矩阵与向量31A的列向量组β,=|0β, =2β, =-1β =4LO]0504个三维向量必线性相关，而其中ββ线性无关所以A的列秩也等于3

第二章 矩阵与向量 1 2 3 4 1 1 3 1 0 2 1 4 0 0 0 5 A                                                  的列向量组 4个三维向量必线性相关，而其中β1 β2 β4线性无关， 所以A的列秩也等于3

第二章矩阵与向量2.矩阵的初等行列变换对矩阵的行列秩的影响。定理1初等行变换不改变矩阵的行秩证明：设m×n矩阵A的行向量组αi,αz,…，αm，且ααα,+ka;α;r;+krj=BA=αQ1

第二章 矩阵与向量 定理1 初等行变换不改变矩阵的行秩. 证明： 2.矩阵的初等行列变换对矩阵的行(列)秩的影响。 1 2 , , 设m n A  矩阵 的行向量组   ， m ，且 1 1 ~ i j i j i r kr j j m m k A B                                                               

第二章矩阵与向量由α, = αiα, =(α; +kα,)-kαdm=αm可知，矩阵A的行向量组可由B的行向量组线性表示显然，矩阵B的行向量组可由A的行向量组线性表示所以，矩阵A、B的行向量组等价从而矩阵A、B的行向量组的秩相同

第二章 矩阵与向量 1 1 ( ) i i j j m m k k              由 可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性表示. 所以，矩阵A、B的行向量组等价. 从而矩阵A、B的行向量组的秩相同

第二章矩阵与向量定理2初等行变换不改变矩阵列向量间的线性关系例3 设矩阵A=其列向量6α1,α2,α3,α,间有线性关系: α =α, + 2αz -α3矩阵B由矩阵A经过有限次初等行变换得到证明B的列向量β,β,,β3,β间也有线性关系β = β, +2β, -β

第二章 矩阵与向量 定理2 初等行变换不改变矩阵列向量间的线性关系. 1 2 3 4 4 1 2 3 1 2 3 4 4 1 2 3 1 1 3 0 3 0 2 1 5 6 0 2 4 , , , 2 . , 2 A B A B                                   例 设矩阵 其列向量 间有线性关系： 矩阵 由矩阵 经过有限次初等行变换得到 证明 的列向量 间也有线性关系

第二章矩阵与向量解：对矩阵A作初等行变换如下：03333+3r23-6r52021519019-1640r-3r3100225一r2+r3001

第二章 矩阵与向量 解：对矩阵A作初等行变换如下 ： 3 1 6 1 1 3 0 1 1 3 0 0 2 1 5 ~ 0 2 1 5 6 0 2 4 0 6 16 4 r r                          3 2 3 1 1 3 0 ~ 0 2 1 5 0 0 19 19 r r              3 1 ( ) 19 1 1 3 0 ~ 0 2 1 5 0 0 1 1 r               31 2 3 3 1 1 0 3 ~ 0 2 0 4 0 0 1 1 r r r r             

第二章矩阵与向量00301ri-r200:B2一211容易看出，B的列向量β,βz,β3,β,间也有线性关系β4= β,+2β,-β3推论初等行变换不改变矩阵的列秩

第二章 矩阵与向量 2 1 2 1 1 0 3 ~ 0 1 0 2 0 0 1 1 r             1 2 1 0 0 1 ~ 0 1 0 2 0 0 1 1 r r B              1 2 3 4 4 1 2 3 , 2 . B            容易看出， 的列向量 间也有 线性关系 推论 初等行变换不改变矩阵的列秩