《高等数学》课程教学资源（课件讲稿）第三章_3.2洛必达法则

3.2洛必达法则0型未定式01型未定式和“002其他类型的未定式

01 02 其他类型的未定式 “ 0 0 ” 型未定式和“ ∞ ∞ ” 型未定式 3.2 洛必达法则

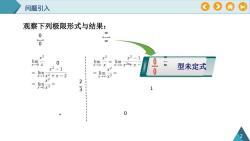
OAP问题引入观察下列极限形式与结果：80011-l1"0"80+2+20limlimlim0b0x-0 xx-=00 x20+ xx-→00x型未定式x2 10=limlimx=1x2+x-2X=00x3+22=lim=X-0x313000--

2 问题引入 观察下列极限形式与结果： " 0 0 " 0 2 3 ∞ ∞ 1 0 " ∞ ∞ " 型未定式 , ∞ ∞

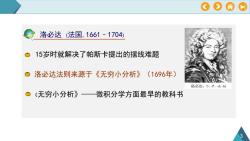
?洛必达（法国，1661-1704)15岁时就解决了帕斯卡提出的摆线难题洛必达法则来源于《无究穷小分析》（1696年）必达，G.-F.-A.de《无穷小分析》一一微积分学方面最早的教科书

3 洛必达法则来源于《无穷小分析》（1696年） 15岁时就解决了帕斯卡提出的摆线难题 《无穷小分析》——微积分学方面最早的教科书 洛必达 (法国,1661–1704)

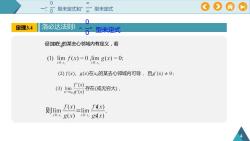
000OAO型未定式型未定式和0000洛必达法则定理3.4” 型未定式设（0在的某去心邻域内有定义，若(1) lim f(x) = 0 ,lim g(x)= 0:XRXXRX,(2)f(x)、g(x)在xo的某去心邻域内可导，且g'(x)± 0;f'(x)存在（或无穷大），(3)limx-xo g'(x)fdx)f(x)则lim-limgdx)xRXog(x)xRX

4 设ᵆ(ᵆ)、ᵆ(ᵆ)在ᵆ0的某去心邻域内有定义，若 定理3.4 “ 0 0 ” 型未定式 一、 “ 0 0 ” 型未定式和“ ∞ ∞ ” 型未定式

OAO定义辅助函数定理3.4证明(f(x),g(x),x+xo，x±xofi(x) :91(x)00x=xox=xo在xo的去心邻域内任取一点x，在以xo与x为端点的区间上，fi(x)与g1(x)满足柯西中值定理的条件，则有f'()f(x)f(x) -f(xo)（在以x.与x之间）g'(5)g(x)g(x) - g(xo)f(x)f'(x)f'(3)f'(x)故limlim当x→x时，5→xo,limlimx-xo g(x)x-xo g'(x)6-x0 g'(3)x-xo g(x)

5 定理3.4证明 定义辅助函数

OAx3 - 12x + 16例7Im x3 - 22* 4++80x3- 12x+16(可)o解limx=2x3-2x2-4x+803x2-12lim(可)x=23x2-4x-46x= limx=26x -43= 2O

6 (  00  ) 例 1 解 (  00  ) = 32

OAP0tanx -xlim(可)x2sinxx-0tanx-x解limO无穷小替换x2sinxx-→00tanx -x(可)= limx3x-0sec2x - 1=lim3x2x-0tan?x无穷小替换=lim3x2x→01=3

7 (  00  ) 例 2 解 = 13 (  00  ) 无穷小替换 无穷小替换

OOAg(x) - cosxx±0.已知f(x)x其中g(x)有二阶连续导数，且g(0）=1，x=0a,C解O(1)确定a的值，使f(x)在x=0点连续；(2)求f(x).f(x) -f(0)g(x) - cosx(2)f'(0) = lim(1) limx-0x-0xx-00g(x) - cosx - xg(O)(可)g'(x) + sinx= lim= limx2x-01x→00g'(x) + sinx - g'(0)=limg'(x)+limsinx()= limx→0x-→02xx→0=g'(0)+ 0 =f(0) = a"(x) + cosxg"(0) + 1=lim22x→08

8 例 3 解 (  00  ) (  00  )

000OOA型未定式型未定式和“0"f(a+h) +f(a-h) -2f(a)设f"(x)在x=a点附近连续，求极限lim例h2h-→00口解该极限为型未定式，因为存在，则（存在，o"利用洛必达法则，有00f(a+h)+ f(a- h)- 2f(a)fda+h)-fda-h)limlimh?2hh?0h?00f"(a+h)+f"(a-h)A=f"(a)lim2h-→09

9 一、 “ 0 0 ” 型未定式和“ ∞ ∞ ” 型未定式 该极限为“ 0 0 ” 型未定式，  因为ᵆ″(ᵆ)存在，  则ᵆ′(ᵆ) 存在，   利用洛必达法则，  有 例 4 解

000OOA型未定式型未定式和“0"f(a + h) +f(a-h)-2f(a)例5设f"(a)存在，求极限limh2h-→0?00解该极限为“”型未定式，因为存在，则存在，利用洛必达法则和导数的定义有0f(a+h)+ f(a- h)- 2f(a) 0fda+h)- fda-h)limlimh?2hh?0h?0fda+h)- fda)da- h)- fda)f'(a+h) -f'(a)+f'(a)-f'(a-h)= limlimlim2hh-→02h2hh?0hR011fda+h)- fda)faa- h)- fda)=limlim= 2+ 2= 2h-2hh?0hOC

10 一、 “ 0 0 ” 型未定式和“ ∞ ∞ ” 型未定式 该极限为“ 0 0 ” 型未定式，  因为ᵆ″(ᵆ) 存在，  则ᵆ′(ᵆ) 存在，   = 1 2ᵆ″(ᵆ) + 1 2ᵆ″(ᵆ) = ᵆ″(ᵆ). 例 5 解 利用洛必达法则和导数的定义有