《高等数学》课程教学资源（matlab及案例）10人口预测与数据拟合

实验10曲线拟合与插值

实验 10 曲线拟合与插值

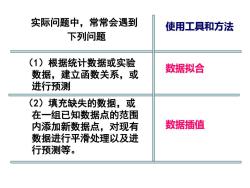
实际问题中，常常会遇到使用工具和方法下列问题（1）根据统计数据或实验数据拟合数据，建立函数关系，或进行预测（2）填充缺失的数据，或在一组已知数据点的范围数据插值内添加新数据点，对现有数据进行平滑处理以及进行预测等

实际问题中，常常会遇到 下列问题 （1）根据统计数据或实验 数据，建立函数关系，或 进行预测 （2）填充缺失的数据，或 在一组已知数据点的范围 内添加新数据点，对现有 数据进行平滑处理以及进 行预测等。 使用工具和方法 数据拟合 数据插值

实验13人口数量预测模型实验实验目的1、学会用MATLAB软件进行数据拟合2、掌握在最小二乘意义下数据拟合的理论和方法初步掌握3、通过对实际问题的分析和研究，建立数据拟合数学模型的方法

实验13 人口数量预测模型实验 2、掌握在最小二乘意义下数据拟合的理论 和方法. 1、学会用MATLAB软件进行数据拟合 3、通过对实际问题的分析和研究，初步掌握 建立数据拟合数学模型的方法 实验目的

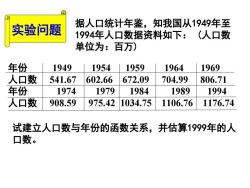
据人口统计年鉴，知我国从1949年至实验问题1994年人口数据资料如下：（人口数单位为：百万）年份19691949195419591964人口数704.99541.67602.66672.09806.71年份19791984198919941974人口数908.59975.421034.751106.761176.74试建立人口数与年份的函数关系，并估算1999年的人口数

据人口统计年鉴，知我国从1949年至 1994年人口数据资料如下： (人口数 单位为：百万) 试建立人口数与年份的函数关系，并估算1999年的人 口数。 实验问题 年份 1949 1954 1959 1964 1969 人口数 541.67 602.66 672.09 704.99 806.71 年份 1974 1979 1984 1989 1994 人口数 908.59 975.42 1034.75 1106.76 1176.74

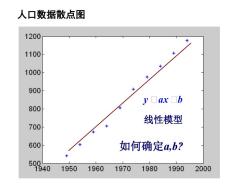
人口数据散点图120011001000900yaxb800线性模型700600如何确定a,b?5001940195019601970198019902000

线性模型 如何确定a,b? 人口数据散点图

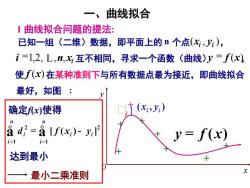
一、曲线拟合1曲线拟合问题的提法：已知一组（二维）数据，即平面上的n个点xi，yi），i=1,2,L,n,x互不相同,（曲线)y=f(x)寻求一个函数使f(x)在某种准则下与所有数据点最为接近，即曲线拟合最好，如图：(x;,J,)确定f(x)使得nnad, =a[f(x)- yPJ= f(x)i=1i=1达到最小+x最小二乘准则

1 曲线拟合问题的提法: 已知一组（二维）数据，即平面上的 n 个点( , ) i i x y ， n xi i =1,2, L, , 互不相同，寻求一个函数（曲线）y = f (x)， 使 f (x)在某种准则下与所有数据点最为接近，即曲线拟合 最好，如图 : x y 0 + + + + + + + + 一、曲线拟合 确定f(x)使得 达到最小 最小二乘准则

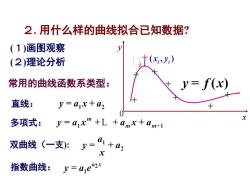
2.用什么样的曲线拟合已知数据？（1）画图观察y+(x,,y,)(2）理论分析常用的曲线函数系类型：y= f(x)直线：y=ax+az+0x多项式：y=a,x" +L +amx+am+1a双曲线(一支):+a2y=xy =a,e"2x指数曲线：

２. 用什么样的曲线拟合已知数据? 常用的曲线函数系类型： (１)画图观察 (２)理论分析 指数曲线： 双曲线（一支): 多项式： 直线： x y 0 + + + + + + + +

3拟合函数中参数的确定以f(x)=a,x+a,为例,即确定a，a,使得J(aia？[ax,az,达到最小。ioi得到关为此，只需利用极值的必要条件10(k 1,2)2[a,x,a,)y,Ix,0a1,a2n2[a,x,a,y,]0il

３ 拟合函数中参数的确定

二、人口预测的线性模型对于开始提出的实验问题，代如数据，计算得a, =15,a, =- 27754从而得到人口数与年份的函数关系为y = 15x - 27754线性预测模型把x=1999代如，估算出1999年的人口数为J=1252.1（百万）=12.52亿1999年实际人口数量为12.6亿

二、人口预测的线性模型 对于开始提出的实验问题, 代如数据，计算得 从而得到人口数与年份的函数关系为 把x=1999代如，估算出1999年的人口数为 y=1252.1（百万）＝12.52亿 1999年实际人口数量为１２.６亿。 线性预测模型

三、人口预测的Malthus模型英国人口学家Malthus根据百余年的人口统计资料，于1798年提出了著名的人口自然增长的指数增长模型。基本假设：人口（相对)增长率r是常数x(t)～时刻t 的人口,仁0时人口数为xdx= rx,P x(t)= xpertdt指数增长模型1 x(0) = xo实际中，常用 x(t)=ea+bt Inx(t)=α+bt

英国人口学家Malthus根据百余年的人口统计资 料，于1798年提出了著名的人口自然增长的指数增 长模型。 三、人口预测的Malthus模型 基本假设 : 人口(相对)增长率 r 是常数 x(t) ~时刻t 的人口, t=0时人口数为x0 指数增长模型 实际中，常用