《高等数学》课程教学资源（课件讲稿）第四章_4.5有理函数的积

高等数学（上册）（慕课版）第四章不定积分第五讲有理函数的积分主讲教师人民邮电出版社RISS&HTOTRES

主讲教师 | 第五讲 有理函数的积分 高等数学（上册）（慕课版） 第四章 不定积分

本讲内容01有理函数的积分02三角有理函数的积分

本讲内容 01 有理函数的积分 02 三角有理函数的积分

A、有理函数的积分1.有理函数的相关概念P(x)称为有理函数,也称为有理分式两个多项式函数的商Q(x)有理分式的一般表达式为P(x)a,x"+a,x"-I +L +an.x+aQ(x) box"+bx"-+L +bm-ix+b,其中m,n为自然数；ao,a,,L,a,及bo,b,,L,b,都是实数，并且a。10,b. 1 0

一、有理函数的积分 3 1.有理函数的相关概念

OA、有理函数的积分在有理分式中当 n<m时,称之为真分式，例如x+3真分式(n<m);x2- 5x+6当n3m时，称之为假分式，例如x+3x2+3假分式(n3 m)x2- 5x+6x2- 5x +6

一、有理函数的积分 4

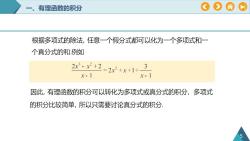
7有理函数的积分根据多项式的除法，任意一个假分式都可以化为一个多项式和一个真分式的和例如2x-x2+232=2x2+x+1+x- 1x-1因此，有理函数的积分可以转化为多项式或真分式的积分，多项式的积分比较简单，所以只需要讨论真分式的积分F

一、有理函数的积分 5

OOAA有理函数的积分2.真分式的积分P(x)真分式！可以被分解为如下最简分式的和：Q(x)B,AP(x)B,A+1Q(x)(x-b)(x- b)°(x-a)X-C-B,Mx+NM,x+ N.M,x+N,x-bx? + px+q(x? + px +q)(x? + px +q)Rx+S.Rx+ S,Rx+S,+L -x+rx+s(x2 +rx+s)"(x2 +rx+s其中A,L,A,BL,Bh,M,L,M.M,LN,L.R,L,Rm,S,L,Sm等为待定常数，利用待定系数法可以将所有的系数确定

一、有理函数的积分 6 2.真分式的积分

OOA0、有理函数的积分x+3例求不定积分0.5x+6°dx.1x+3是真分式，可分解为最简分式之和被积函数o解x2- 5x+6求A，A,还可以用特殊值法：x+3x+3A,Ax2- 5x+6设x+3=A(x-3)+A,(x-2)x-3(x- 2)(x- 3)x- 2将x=2代入，得A=-5其中A，A为待定系数将x=3代入，得A=6在分解时两端消去分母得x+3= A(x- 3)+A(x- 2)=(A + A,)x+(-3A - 2A)iA +A, =1比较x的各次幂的系数得i-3A- 2A, =3解得A=-5,A=6

一、有理函数的积分 7 例 1 解

>有理函数的积分从而接前56x+31x2-5x+6x- 3x- 2所以x+36dx10.5x+6x- 3=-5lnx-2+6nx-3+C8

一、有理函数的积分 8 接前

OOA、有理函数的积分x求不定积分x例(x +2)(x+3)福先将被积函数分解为最简分式之和o解特殊值法：AxA AX=-2, A =-2.x+2x+3(x+3)(x +2)(x +3)2X=-3,A =3,通分得X=0,A,=2.x= A(x+3)2 + A(x+2)(x+3)+A(x+2)即x=(A +A,)x2+(6A +5A, +A)x+(9A +6A,+2A)iA +A =0比较x的各次幕的系数得6A+5A,+A,=119A, +6A, +2A, =0S

一、有理函数的积分 9 例 2 解

有理函数的积分解得A=-2，A,=2,A=3,从而接前23-2x(x +3)2(x +2)(x +3)2x+2x+3所以x+23=-2lnx+2+2lnx+Cx+3

一、有理函数的积分 10 接前