《高等数学》课程教学资源（课件讲稿）第四章_4.4分部积分法

高等数学（上册）（慕课版）第四章不定积分第四讲分部积分法主讲教师人民邮电出版社RISSAHTOTRES

主讲教师 | 第四讲 分部积分法 高等数学（上册）（慕课版） 第四章 不定积分

OOA第四讲分部积分法设u=u(x),V=v(x)在区间I上都有连续的导数，则有定理4.5du(x)vx)dx = u(x)v(x) - dudx)v(x)dx简记为ovdx=v-udx或udy= uv- Oy du上述公式被称为分部积分公式如果求vdx有困难，而求dx比较容易时，分部积分公式就可以起注到化难为易的转化作用

第四讲 分部积分法 2 定理4.5 注

A7第四讲分部积分法分部积分法应用的基本步骤为vdx = dv= uv- oydu = - ouadx分部积分法的关键在于适当地选择u和dv.选取u和dy一般要考虑下面两点：(1)由vax)dx要容易求得v;(2)oydu要比dv容易积分

第四讲 分部积分法 3

OA第四讲分部积分法求不定积分orarctanxdx.4x2则选u=arctanx, vo解2xOrarctan.xdx=oarctanxcarctan xarctan2xarctanxarctanx22arctan x)+Carctanx2如果被积函数是幂函数与反三角函数或对数函数的乘积，可用注分部积分法，并选反三角函数或对数函数为u，幂函数选作v

第四讲 分部积分法 4 例 1 解 注

OOA第四讲分部积分法求不定积分iecosxdx例令=e"cosxdx，则有选u=cosx,v=e解I = ocosx de"=e"cosx- e'dcos x=e"cosx+ oe' sin x dx =e* cosx+ osin x de选u=sinx,v=e原式=e"cosx+e'sinx-e"dsinx=e'cosx+e'sinx- e" cosxdx出现变量再现=e' cosx+e'sinx- I所以2I =e" cosx+e" sinx+C,即-e'(cosx+sin x)+C2

第四讲 分部积分法 5 例 2 解

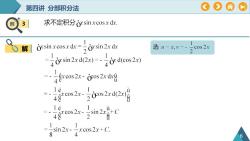
A第四讲分部积分法求不定积分orsinxcosxdxorsin x cos x dx =orsin2xdx选u-x.V--cos2x解OObr sin2x d(2x) :d(cos2x)rocos2xdxxcos2x-4°Té1ercos2x72.x48021léu4grcos2r.sin2xa+uu21sin2xxcos2x+(84

第四讲 分部积分法 6 例 3 解

OAP第四讲分部积分法求不定积分secxdx.I = osec x dx = osec x xsec x dxO解= osec x d tan x = sec x tan x - an x d sec x选u=secx,y=tan x= sec x tan x- otan x sec x dx= secx tan x- (sec x-1) xsec x dx= sec x tan x- osec x dx + osec x dx= sec x tan x - I +In secx + tan x

第四讲 分部积分法 7 例 4 解

第二讲第二换元积分法接前即2I = sec x tan x + ln sec x+ tan x+C所以-In sec x + tan x+Csecxtanx+228

第二讲 第二换元积分法 8 接前

高等数学（上册）（慕课版学海无涯，祝你成功！主讲教师人民邮电出版社RISS&HTOTRES

主讲教师 | 学海无涯，祝你成功！ 高等数学（上册）（慕课版）