《高等数学》课程教学资源（课件讲稿）第二章_2.3隐函数及参数方程确定的函数的求导

第三节隐函数及由参数方程确定的函数求导01隐函数的导数02对数求导法03由参数方程确定的函数的导数

01 隐函数的导数 02 对数求导法 03 由参数方程确定的函数的导数 第三节 隐函数及由参数方程 确定的函数求导

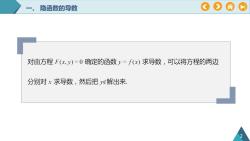
隐函数的导数对由方程F(x.)=0 确定的函数y=f(x)求导数，可以将方程的两边分别对x求导数，然后把ye解出来

一、 隐函数的导数 2

?隐函数的导数例1求由方程xy=ex+y所确定的隐函数y=y(x)的导数y解D方程两边对x求导，得y+xy=ex+y(1+y)ex+y-y解得y!x-ex+y

一、 隐函数的导数 3 例 1 解

OOA隐函数的导数例2求由方程x-y+=siny=0所确定的隐函数y=y(x)的二阶导数y20解方程两边对x求导，得1-ye+=cosyxye=022解得ye=2- coSJ2- 2 sin y xye上式两边再对x求导，V=代入得再将ve2- cosJ(2 - cos y)-4sinyve(2 - cosy)

一、 隐函数的导数 4 例 2 解

OOAA隐函数的导数例求由方程y=tan(x+y)所确定的隐函数的二阶导数y方程两边对x求导，得，e=sec(x+y)(1+)=(1+)(1+)，解D1+yy = tan(x +y)解得ye1- (1+2)2ye上式两边再对x求导，V1 代入得再将vo12ye_. 2(1+y)=-2csc (x+ y)cot'(x+ y).veJ3Y

一、 隐函数的导数 5 例 3 解

OAH隐函数的导数方程/=x（x>0,>0)，确定函数y=f(x），求例dr方程y=x两边分别对x取自然对数解O避免商的求导公式得=Iny=一Inx，即ylny=xlnx-1等式两边对x求导，得(n y+)崇=In x+1,dxdyInx + 1即In y+1dx

一、 隐函数的导数 6 例 4 解 避免商的 求导公式

CO7隐函数的导数In x +1dy接前dxIn y+1再对x求导数，得d(ln y+1)- (ln x+1)×ydxdx?(ln y+1)2y(In y+1)2 - x(In x +1)2xy(ln y+1)3

一、 隐函数的导数 7 接前

O0隐函数的导数例已知函数f(u)具有二阶导数，且fdO)=1，函数y=y(x)由方程d2dzy-xel=1所确定.设z=f(lny-sinx），求）dxdx由方程y- xe-1=1p y(O)=1,解A两边对x求导，得ye-e"-1-xeye=0pyO)=1,上式两边再对x求导，y-2e-ye-x(eyge=0pyu0)=2，现由z=f(lny-sinx)可得8

一、 隐函数的导数 8 解 例 5

0O#0隐函数的导数例已知函数f(u）具有二阶导数，且fO)=1，函数=(x）由方程d’zdz求y-xe-l=1所确定.设z=f(lny-sinx)dxdxdz解fc(ln y- sin x)(-ye- cosx) pf(0)"0=0dx2d’zfadln y- sin x)(-ye- cos x) + fdln y- sin x)(--(v92ve+ sinxdx? f0)' 0+ fd0)(- 1+2) =1.dxS

一、 隐函数的导数 9 解 例 5

第三节隐函数及由参数方程确定的函数求导隐函数的导数01对数求导法0203由参数方程确定的函数的导数

隐函数的导数 对数求导法 03 由参数方程确定的函数的导数 01 02 第三节 隐函数及由参数方程 确定的函数求导