《高等数学》课程教学资源（matlab及案例）11追击问题与微分方程数值解

实验11缉私艇追击走私船

实验 11 缉私艇追击走私船

实验目的1(1)提高学生根据实际问题建立微分方程模型的能力;(2)学习求微分方程解析解与数值解的方法(3)学习简单的计算机仿真方法。2实验问题海上边防缉私艇发现距C公里处有一走私船正以与速沿垂直于他们连线的直线行驶缉私艇立即以最大速度追赶,在雷达的引导下，缉私艇C的方向始终指向走私船。问：缉私艇何时追赶上走私船？并求出私艇追赶的路线

1 实验目的 (1)提高学生根据实际问题建立微分方程模型的能力； (2)学习求微分方程解析解与数值解的方法; (3)学习简单的计算机仿真方法。 海上边防缉私艇发现距c公里 处有一走私船正以匀速a沿 垂直于他们连线的直线行驶, 缉私艇立即以最大速度b追 赶,在雷达的引导下，缉私艇 的方向始终指向走私船。问: 缉私艇何时追赶上走私船? 并求出缉私艇追赶的路线。 2 实验问题 c

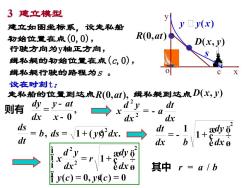
3建立模型yy y(x)建立如图坐标系。设走私船R(0,at)初始位置在点(0,0),D(x,y)行驶方向为y轴正方向，缉私艇的初始位置在点(c, 0),0Cx缉私艇行驶的路程为S设在时刻t：缉私艇到达点D(x,J)走私船的位置到达点R(0,at),dyy-atdtdy则有xdx?x- 0dxdx2dsdt, ds = 1+(y9'dx. b.dtdxbdx o3daedy0dxédx o其中 ｒ=a/b1 y(c) = 0, ydc) = 0

3 建立模型 o c x y 建立如图坐标系，设走私船 初始位置在点(0,0)， 行驶方向为y轴正方向， 缉私艇的初始位置在点(c,0)， 缉私艇行驶的路程为s 。 设在时刻t： 走私船的位置到达点 缉私艇到达点

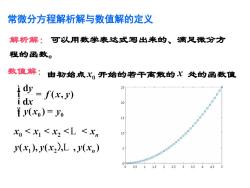
常微分方程解析解与数值解的定义解析解：可以用数学表达式写出来的、满足微分方程的函数。数值解：由初始点X.开始的若干离散的X处的函数值25dy= f(x,y)i dx2011 y(xo) = yooOO152000Xo<Xi<X2<L <Xn108e200-00y(x,),y(x,),L (xn)58990690060909090000000.51.522.53.55013Y4.5

常微分方程解析解与数值解的定义 解析解： 可以用数学表达式写出来的、满足微分方 程的函数。 数值解：由初始点     开始的若干离散的     处的函数值

4 模型求解d2aedy o(1)人工求解析解Sdx odxd'ydydpy(c) = 0, ydc) = 0p,今dx?dxdx其中r=a/bdxdpa：走私船速度x/1+pb：缉私挺速度1 p(c) = 0aer o/1+pp+.aec odyécoOexoe2-.dx0aec或 p-1+p2 y(c) = 0éxo

4 模型求解 (1) 人工求解析解 令： 或

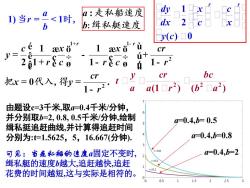
dl福a：走私船速度21)当r="<1时,2b:缉私艇速度bvc1+1Uaex o0craexu+231+r8c0白0bcVcrcr把x=0代入，得ya2(b-aa(1由题设c=3千米,取a=0.4千米/分钟并分别取b=2.0.8.0.5千米/分钟,绘制a=0.4,b= 0.5缉私挺追赶曲线，并计算得追赶时间a=0.4.b=0.8分别为：t=1.5625，5，16.667(分钟)r=0.8a=0.4,b=2可见：当走私船的速度固定不变时=0.5缉私艇的速度b越大,追赶越快,追赶r=0.2花费的时间越短,这与实际是相符的。0.51.522.501

由题设c=3千米,取a=0.4千米/分钟， 并分别取b=2, 0.8, 0.5千米/分钟,绘制 缉私挺追赶曲线,并计算得追赶时间 分别为:t=1.5625，5，16.667(分钟). 可见：当走私船的速度a固定不变时, 缉私艇的速度b越大,追赶越快,追赶 花费的时间越短,这与实际是相符的。 a=0.4,b=2 a=0.4,b=0.8 a=0.4,b= 0.5

éer odyaec a：走私船速度2)当r=">1时,ec-dxb:缉私挺速度exoseC0b0y(c)1+UcrCaer oaecu2+rlexoéct0当x?0时，?+，缉私艇不可能追赶上走私船。22xo1 aex3)当r=1时,clnceeV212cC0当x0时，J?+，缉私艇不可能追赶上走私船。容易验证，模型结论与事实相符

当 时， ，缉私艇不可能追赶上走私船。 当 时， ，缉私艇不可能追赶上走私船。 容易验证，模型结论与事实相符

(2)用MATLAB软件求解析解MATLAB软件提供的解常微分方程及方程组解析解的指令是dsolve。可以用于求解存在解析解的常（组）。调用格式如下：微分方程S = dsolve(eqn)S = dsolve(eqn,cond)[yl,...,yN] = dsolve(求微分方程y=X+Xy的通解例1程序：运行结果：syms y(x)y=eqn = diff(y,x) == x+x*y;C1*exp(x^2/2) - 1y=dsolve(eqn)

（2）用MATLAB软件求解析解 MATLAB软件提供的解常微分方程及方程组解析 解的指令是dsolve，可以用于求解存在解析解的常 微分方程（组）。调用格式如下:                  S = dsolve(eqn)                  S = dsolve(eqn,cond)                  [y1,.,yN] = dsolve(_) 例1 求微分方程 的通解 程序： syms y(x) eqn = diff(y,x) == x+x*y; y=dsolve(eqn)  运行结果： y = C1*exp(x^2/2) – 1

d'y例2的通解。求微分方程aydt?程序：运行结果：syms y(t) a %注意变量之间不能用逗号ySol(t) =C2*exp(-eqn = diff(y,t,2) == a*y;a^(1/2)*t) +ySol(t) = dsolve(eqn)C3*exp(a^(1/2)*t)id'yay例3的解。求微分方程dt?■1 y(0) = b, yd(0) = 1程序：syms y(t) a b运行结果：eqn = diff(y,t,2) == a^2*y:ySol(t) =Dy = diff(y,t);(exp(a*t)*(a*b + 1)/(2*a) +cond = [y(0)==b, Dy(0)==1];(exp(-a*t)*(a*b - 1)/(2*a)ySol(t) = dsolve(eqn,cond)

例2 求微分方程 的通解。 程序： syms y(t) a %注意变量之间不能用逗号 eqn = diff(y,t,2) == a*y; ySol(t) = dsolve(eqn)  运行结果： ySol(t) =C2*exp(- a^(1/2)*t) +  C3*exp(a^(1/2)*t) 例3 求微分方程 的解。 程序： syms y(t)  a  b eqn = diff(y,t,2) == a^2*y; Dy = diff(y,t); cond = [y(0)==b, Dy(0)==1]; ySol(t) = dsolve(eqn,cond)  运行结果： ySol(t) =  (exp(a*t)*(a*b + 1))/(2*a) +  (exp(-a*t)*(a*b - 1))/(2*a)

i dxyidt例4的通解。求微分方程组dy1-x1dt程序：syms x(t) y(t)eqns = [diff(x,t)==y, diff(y,t)==-x];[xSol(t) ySol(t)] = dsolve(eqns)运行结果：xSol(t) =C7*cos(t) + C6*sin(t)ySol(t) =C6*cos(t) - C7*sin(t)

例4 求微分方程组 的通解。 程序： syms x(t)  y(t) eqns = [diff(x,t)==y, diff(y,t)==-x]; [xSol(t) ySol(t)] = dsolve(eqns)  运行结果： xSol(t) =C7*cos(t) + C6*sin(t) ySol(t) =C6*cos(t) - C7*sin(t)