《高等数学》课程教学资源（课件讲稿）第三章_3.3泰勒中值定理

3.3泰勒中值定理01泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

麦克劳林公式 泰勒中值定理 03 几个重要初等函数的麦克劳林公式 02 04 泰勒公式的应用 01 3.3 泰勒中值定理

CO7问题提出一、问题提出由函数的微分，得到f(x)的近似公式f(x) f(xo)f (xo)(x x)不足：1、精确度不高；2、误差不能估计问题：寻找函数P,(x),使得f(x)》 P,(x)误差R,(x)=f(x)-P,(x)可估计

问题提出 2 一、问题提出 不足: 问题: 1、精确度不高； 2、误差不能估计

COAO问题提出设函数f(x)在含有x.的开区间(a,b)内具有直到(n+1)阶导数，P.(x)为多项式函数P,(x)aa(xx)a,(xx,)a,(xx)满足: P((x)= f(")(x) k = 0,1, .,nao =f(xo)Pn(xo)= f(xo)ai =f'(xo)pn(xo)= f'(xo):...k)(xo)Pn(k)(xo) = f(k)(xo)akk!

问题提出 3 满足：

O泰勒中值定理定理3.6（泰勒中值定理）设函数f(x)在含有x。的某个开区间(a,b)内具有直到(n+I）阶导数，则对任意xi（a,b）有泰勒公式aXof(x)=f(x)+ fax)(x-x.(x-xo)" +R,(x),(3.1)2!n!Y其中R.(x)(n+I)!其中x介于x与x之间拉格朗日余项

一、泰勒中值定理 4

O泰勒中值定理(x-x)"+1 (x在x,与x之间)拉格朗日形式的余项R.(x)(n +1)!M24R-(n+1)!(n+1)!佩亚诺形式的余项oa所以f(x)=- x)* +o[(x - x)"]Yk!k=0L

一、泰勒中值定理 5

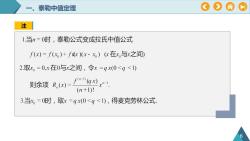
OA一、泰勒中值定理注1.当n=0时，泰勒公式变成拉氏中值公式f(x)=f(x)+fdx)(x- x） (x在x与x之间)2.取x，=0,x在0与x之间，令x=qx(0<q<1)则余项 R,(at)= L"(qx)x"+1(n+1)!3.当x，=0时，取x=gx(0<q<1)，得麦克劳林公式

一、泰勒中值定理 6 注

3.3泰勒中值定理01泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

麦克劳林公式 泰勒中值定理 03 几个重要初等函数的麦克劳林公式 01 04 泰勒公式的应用 02 3.3 泰勒中值定理

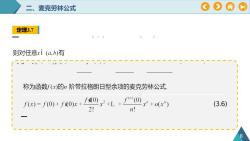
OA麦克劳林公式定理3.7则对任意xi(a,b)有X称为函数f(x)的n阶带拉格朗日型余项的麦克劳林公式fao)70(3.6)f(x)=f(O)+ fa0)x+ox2!n!

二、麦克劳林公式 8 定理3.7

CO7二、麦克劳林公式由(3.5)和(3.6)可得近似公式f(x)》 f(0)+ Fα0)x+Tα)02!n!(0a0右端多项式记作P(x）=f(O)+fα0)x2!n!称为f(x)的n阶麦克劳林多项式，其系数为(k =0,1.2,L n),k!M误差估计式：R（x)n+S

二、麦克劳林公式 9

3.3泰勒中值定理01泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

麦克劳林公式 泰勒中值定理 几个重要初等函数的麦克劳林公式 01 02 04 泰勒公式的应用 03 3.3 泰勒中值定理