《线性代数》课程教学资源（课件讲稿，C）第三章 3-4分块矩阵

第三章矩阵的运算第四节分块矩阵

第三章 矩阵的运算 第四节 分块矩阵

第三章矩阵的运算一、分块矩阵的概念1.定义设A是一个矩阵，在A的行和列之间加上一些线，将其分成若于小块，每一小块称为A的子块以子块为元素的形式上的矩阵称为分块矩阵a13a14a1215aaaaaa.2325212224A=(13)(132(133a(3534(41A(143(1A445A.A13则A可记作ZAA23

第三章 矩阵的运算 一、分块矩阵的概念 1.定义 设A是一个矩阵，在A的行和列之间加上一 些线，将其分成若干小块，每一小块称为A的子块. 以子块为元素的形式上的矩阵称为分块矩阵. 31 32 3 11 3 13 14 23 24 1 41 42 5 25 34 43 4 12 2 35 1 4 5 22 4 a a a a a a a a a a a a a a a a a a a A a              则A可记作 21 1 12 3 1 2 2 13 A 2 A A A A A   A     

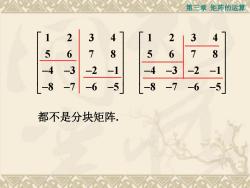
第三章 矩阵的运算3223A478568567-3-2-2-3-4-1-17-7-6-5-6-8-7-5-8都不是分块矩阵

第三章 矩阵的运算 1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5                     1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5                     都不是分块矩阵

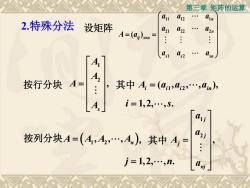
第三章矩阵的运算anay2ain2.特殊分法设矩阵a21a2a2nA=(a).a1sSsnAlAA=按行分块其中 A,=(ai,ai2,,ain)高i =1,2,..,s.ara2j按列分块A=(A,A,,A,),其中 A, =j = 1,2,...,n

第三章 矩阵的运算 2.特殊分法 设矩阵 11 12 1 21 22 2 1 2 ( ) n n ij s n s s sn a a a a a a A a a a a                按列分块 A A A A   1 2 , , , n  ，其中 1 2 , j j j nj a a A a                j n  1,2, , . 按行分块 1 2 , s A A A A              其中 1 2 ( , , , ), A a a a i i i in  i s  1,2, ,

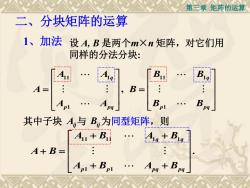
第三章矩阵的运算二、分块矩阵的运算1、加法设A.B是两个m×n矩阵，对它们用同样的分法分块：BBAA190B==4BBpIpq则其中子块A,与 B,为同型矩阵,BAu + B+C1A+B=BBA++pqq

第三章 矩阵的运算 11 1 11 1 1 1 , q q p pq p pq A A B B A B A A B B                       1、加法 设 A, B 是两个m×n 矩阵，对它们用 同样的分法分块: 二、分块矩阵的运算 11 11 1 1 1 1 . q q p p pq pq A B A B A B A B A B                 其中子块 Aij 与 Bij 为同型矩阵，则

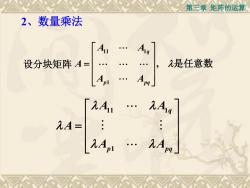
第三章 矩阵的运算2、数量乘法入是任意数设分块矩阵A=pq2A12A42A=A2A1q

第三章 矩阵的运算 2、数量乘法 设分块矩阵 11 1 1 , q p pq A A A A A             是任意数 11 1 1 q p pq A A A A A                

第三章矩阵的运算把矩阵 A=(aik）mxs,B=(bui)xp分块成乘法3、B1Bu41B一BBtq其中A;1,A2,,A,的列数分别等于Btj,B2jB,的行数，那未AB=CCplpq其中C, -AB(i- 1,, p;j-1,.,q)K

第三章 矩阵的运算 11 1 11 1 1 1 1 2 1 2 , , , , , , , , , t q p pt t tq i i it j j tj A A B B A B A A B B A A A B B B                       其 中 的 列 数 分 别 等 于 的 行 数 那 末   11 1 1 1 1, , ; 1, , . q p pq t ij ik kj k C C AB C C C A B i p j q             其 中     3、乘法 把矩阵 ( ) , ( ) A a B b   ik m s kj s p   分块成

第三章 矩阵的运算例1000100:0B=2101O017-11210

第三章 矩阵的运算 1 0 0 0 0 1 0 0 1 2 1 0 1 1 0 1 A               1 0 1 0 1 2 0 1 1 0 4 1 1 1 2 0 B                 例 1

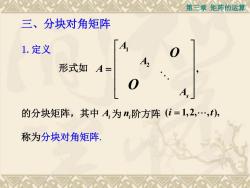
第三章矩阵的运算三、分块对角矩阵A1.定义0A形式如A=0的分块矩阵，其中 A,为 n,阶方阵(i=1,2,,t),称为分块对角矩阵

第三章 矩阵的运算 三、分块对角矩阵 1 2 , s A A A A              O O 称为分块对角矩阵. 形式如 的分块矩阵，其中 Ai 为 ni 阶方阵 ( 1,2, , ), i t  1.定义

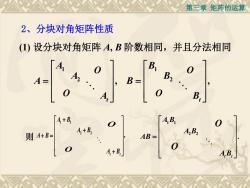
第三章矩阵的运算2、分块对角矩阵性质(1)设分块对角矩阵A,B阶数相同，并且分法相同BAB24B=A=00BA,B,A, +B0A, +B,A,B2则A+B=AB=05A,B

第三章 矩阵的运算 2、分块对角矩阵性质 1 2 , t A A A A            O O 1 2 , t B B B B            O O (1) 设分块对角矩阵 A, B 阶数相同，并且分法相同 则 1 1 2 2 t t A B A B A B A B                  ， O O 1 1 2 2 t t A B A B AB A B              . O O