《线性代数》课程教学资源(课件讲稿,C)第三章 3-2逆矩阵

第三章矩阵的运算$ 3.2逆矩阵
第三章 矩阵的运算 §3.2 逆矩阵

第三章矩阵的运算一、引入在数的运算中,当数a≠0时,有aa-1 =a-'a =1,其中α_ 为a 的倒数,(或称的逆)在矩阵的运算中,单位阵E相当于数的乘法运算中的1那么,对于矩阵A,如果存在一个矩阵A-1,使得AA-1 =A-A= E则矩阵A-称为A的可逆矩阵或逆阵
第三章 矩阵的运算 , 1 1 AA A A E 则矩阵 称为 A 的可逆矩阵或逆阵. 1 A 1, 1 1 aa a a 在数的运算中,当数 a 0 时,有 a a 1 1 其中 为 a 的倒数,(或称 a 的逆) 在矩阵的运算中,单位阵E相当于数的乘法运算中的1, 那么,对于矩阵A,如果存在一个矩阵A -1 ,使得 一、引入

第三章矩阵的运算二、逆矩阵的定义定义3.2.1设A是一个n阶方阵,若存在n阶方阵B,使得 AB=BA=E则称A可逆的,并称B为A的逆矩阵例如,B=AF有AB=BA=E,所以A与B互为逆阵
第三章 矩阵的运算 定义3.2.1 设A是一个n阶方阵, 若存在n阶方阵B, 使得 AB = BA = E 则称 A 可逆的,并称B 为 A 的逆矩阵. 二、逆矩阵的定义 1 2 5 2 , 2 5 2 1 A B 有AB = BA = E ,所以A 与 B 互为逆阵. 例如

第三章矩阵的运算说明:(1)若A是可逆矩阵,则A的逆矩阵是唯一的若设B和C是A的可逆矩阵,则有AB= BA= E, AC =CA=E,可得 B= EB = (CA)B =C(AB)= CE =C所以A的逆矩阵是唯一的,记作A-1B=C=A-1
第三章 矩阵的运算 说明: (1)若A是可逆矩阵,则A的逆矩阵是唯一的 若设B和C是A的可逆矩阵,则有 AB BA E, AC CA E, 可得 B EB CAB CAB CE C. 所以A的逆矩阵是唯一的,记作A -1 1 B C A .
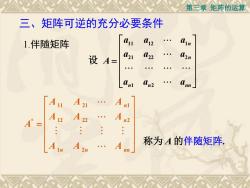
第三章矩阵的运算三、矩阵可逆的充分必要条件al0121.伴随矩阵an1(12272n设A=anlan2annn2称为A的伴随矩阵nn2
第三章 矩阵的运算 11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A 称为 A 的伴随矩阵. 设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a 三、矩阵可逆的充分必要条件 1.伴随矩阵

第三章矩阵的运算21例题1、求矩阵A=的伴随矩阵310A =-2, A2 =6, A3 =1店A= 6 -3 -3A21 = 4, A22 =-3, A23 = -2,-5-21A31 = 1, A32 = -3, A33 = -5
第三章 矩阵的运算 例题1、求矩阵 的伴随矩阵. 1 0 2 3 1 0 1 2 1 A * 2 4 1 6 3 3 1 2 5 A 11 12 13 21 22 23 31 32 33 2, 6, 1 4, 3, 2, 1, 3, 5 A A A A A A A A A

第三章 矩阵的运算Ai=jA+a+12inin0itjA]i=j.A-aziAi +...+a,niInj0itj
第三章 矩阵的运算 1 1 2 2 1 1 2 2 0 0 i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j

第三章矩阵的运算21-141-2AA*=306-3-3-5-2-2A*A=6 -3 -33-215一
第三章 矩阵的运算 * 1 2 1 2 4 1 3 1 0 6 3 3 1 0 2 1 2 5 AA * 2 4 1 1 2 1 6 3 3 3 1 0 1 2 5 1 0 2 A A

第三章 矩阵的运算可得:[IA]011[A|AA*=A*A=AEA只要A±0,就有A(1)A=E)=(一
第三章 矩阵的运算 可得: * * | | 0 0 0 | | 0 0 0 | | A A AA A A A E A 1 1 * * A A A A A E 0 ( ) ( ) A A 只 要 ,就有

第三章矩阵的运算2.定理(可逆的充分必要条件)n阶方阵A可逆→A± O,且A-1A证明已证。"←"(充分)"="(必要)若A可逆,则存在A-,使得AA-1 =E两边取行列式,得 |AA-1 HAIA-1=E=1所以I A↓+ 0
第三章 矩阵的运算 2.定理(可逆的充分必要条件) 1 1 | | 0 | | n A A A A A 阶方阵 可逆 ,且 证明 ""(充分) 已证. ""(必要) 1 1 A A AA E 若 可逆,则存在 ,使得 两边取行列式,得 1 1 | | | || | | | 1 AA A A E 所以 | A| 0
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-1矩阵的运算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-4矩阵的秩.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-4克拉默法则.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-3行列式的计算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-2行列式的性质.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-1n阶行列式的概念.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第二章行列式_第五节 矩阵的秩.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第一章矩阵及其初等变换_第二节 高斯消元法与矩阵的初等变换.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第一章矩阵及其初等变换_第一节 矩阵及其运算.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第四节 实对称矩阵的相似对角化_4.4 实对称矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第二节 矩阵的相似对角化_4.2 矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第三节 n维向量空间的正交性_4.3 n维向量空间的正交性.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第一节 特征值与特征向量的概念与计算_4.1 特征值与特征向量的概念与计算.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第四节 线性变换_6.4 线性变换.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第二节 线性空间的基、维数与坐标_6.2 线性空间的基、维数与坐标.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第三节 欧式空间_6.3 欧式空间.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第一节 线性空间的概念_6.1 线性空间的概念.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第五章 二次型_第二节 正定二次型_5.2 正定二次型.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第五章 二次型_第一节 实二次型及其标准形_5.1 实二次型及其标准形.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_补充_补充.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-3初等矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-4分块矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-1消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-2向量及其线性运算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-3向量组的线性关系.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-1线性方程组有解的判定.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-2齐次线性方程组.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-3非齐次线性方程组.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-九年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-九年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-七年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-七年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-八年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-八年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-六年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-六年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_学生用书(不全)必修3.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_学生用书(不全)必修4.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_教师用书(不全)必修2.pdf
- 《数学教学论》课程教学资源(书籍教材)高中数学教材_新课标_教师用书(不全)必修3.pdf
