《线性代数》课程教学资源(课件讲稿,C)第一章 1-1n阶行列式的概念

线性代数的主要内容解的存在性线性方程组求解解的结构一次方程行列式由高斯消元法引入两个求解工具矩阵一个中心方法:矩阵的初等行变换一个应用:二次曲线和二次曲面的形状判定加油!
一个应用:二次曲线和二次曲面的形状判定 线性方程组求解 解的存在性 解的结构 由高斯消元法引入两个求解工具 行列式 矩阵 一个中心方法:矩阵的初等行变换 一次方程 线性代数的主要内容

(1)aiiXi +ai2X2 = br,(2)a21Xi + a22X2 = b2.用高斯消元法求其解:a1a22X, +[12a2x, =b,a22 (1)×a222 (2)×al2-) a21a12Xi +2ax2 =bza12(aa22 ai2a21) X; = ba22 -b,a12加油!
. , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 1 2 22 (1)a 12 ) (2)a 11 22 12 21 1 1 22 2 12 (a a a a x b a b a ) 用高斯消元法求其解: 21 12 1 22 12 2 2 12 a a x a a x b a 11 22 1 12 22 2 1 22 a a x a a x b a

(1)a11Xi + a12X2 = b1(2)a21Xi +a22X2 =b2.a2ialx +a22aix, =ba1 (2)×a1← (1)×a21ara2ixi +ai2a2ix, = b,a21(aua22 -aiza21) X, =b,al1 -b,a21加油!
. , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 1 2 11 22 12 21 2 2 11 1 21 (a a a a x b a b a ) 21 11 1 22 11 2 2 11 a a x a a x b a 11 (2)a 21 ) (1)a 11 21 1 12 21 2 1 21 a a x a a x b a

二阶行列式定义由四个数排成二行二列(横排称行、竖排称列的数表a11 a12(4)a21 a22数[a1ia22 — a12a2]称为数表(4)所确定的二阶行列式,记为aa12a21a22加油!
由四个数排成二行二列(横排称行、竖排称列) 的数表 (4) 21 22 11 12 a a a a 数 a a a a 11 22 12 21 称为数表(4)所确定的 二阶行列式, 记为 11 12 21 22 a a a a 二阶行列式定义

例1求解二元线性方程组3xi -2x2 =12,2xi + x2 =1.解=3-(-4) = 7 ± 0,D12:-21,-D14DD.-21XL7DD7加油!
例 1 2 1 . 3 2 12 , 1 2 1 2 x x x x 解 2 1 3 2 D 3 ( 4 ) 7 0 , 1 1 12 2 1 D 14 , 2 1 3 12 D 2 21 , DD x 1 1 2 , 7 14 DD x 2 2 3. 7 21 求解二元线性方程组
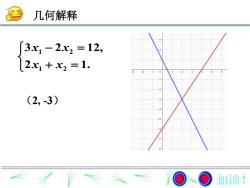
几何解释3xi - 2x2 = 12,2xi + x2 =1.(2, -3)加油!
2 1. 3 2 12, 1 2 1 2 x x x x (2, -3) 几何解释
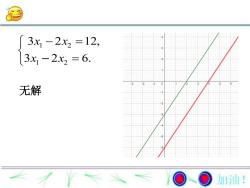
3x -2x2 =12,3x -2x2 = 6.无解加油!
1 2 1 2 3 2 12, 3 2 6. x x x x 无解
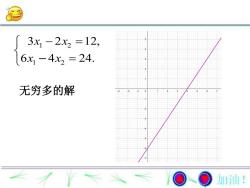
3x, -2x2 =12,6x, -4x2 = 24.无穷多的解加油!
1 2 1 2 3 2 12, 6 4 24. x x x x 无穷多的解

三阶行列式的引出aux+a12x+a3x=ba21Xi +a22X2 +a23X = b2a31Xi +a32x2 +a33X =b加油!
三阶行列式的引出 31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b

a2a3aiix+ai2x2+axg=ba21Xi+a22X2+a23X =b2D=a22a23a21a31x+a32X,+a33Xg=bsa32a3331当D±0时,三元线性方程组的解为DD3D,X.XDDDb.aiai2b,dila13b,a2a13bD, =a22a21b,Da23a2D.b.a22二a23bsa31a32b3a31a33b,a32a33加油!
1 2 3 1 2 3 0 , , D D D D x x x D D D 当 时,三元线性方程组的解为: 11 12 13 21 22 23 31 32 33 a a a D a a a a a a 1 12 13 1 2 22 23 3 32 33 b a a D b a a b a a 31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b 11 1 13 2 21 2 23 31 3 33 a b a D a b a a b a 11 12 1 3 21 22 2 31 32 3 a a b D a a b a a b
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学资源(参考资料,C)线代课件_第二章行列式_第五节 矩阵的秩.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第一章矩阵及其初等变换_第二节 高斯消元法与矩阵的初等变换.pdf
- 《线性代数》课程教学资源(参考资料,C)线代课件_第一章矩阵及其初等变换_第一节 矩阵及其运算.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第四节 实对称矩阵的相似对角化_4.4 实对称矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第二节 矩阵的相似对角化_4.2 矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第三节 n维向量空间的正交性_4.3 n维向量空间的正交性.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第四章 特征值和特征向量_第一节 特征值与特征向量的概念与计算_4.1 特征值与特征向量的概念与计算.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第四节 线性变换_6.4 线性变换.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第二节 线性空间的基、维数与坐标_6.2 线性空间的基、维数与坐标.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第三节 欧式空间_6.3 欧式空间.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第六章 线性空间与线性变换_第一节 线性空间的概念_6.1 线性空间的概念.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第五章 二次型_第二节 正定二次型_5.2 正定二次型.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第五章 二次型_第一节 实二次型及其标准形_5.1 实二次型及其标准形.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_补充_补充.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_第四节 克拉默法则_第四节 克拉默法则.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_第五节 矩阵的秩_第五节 矩阵的秩.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_第二节 行列式的性质与计算_第二节 行列式的性质与计算.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_第三节 拉普拉斯定理_第三节 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第二章 行列式_第一节 行列式的定义_第一节 行列式的定义.pdf
- 《线性代数》课程教学资源(课件讲稿,B)第三章 n维向量空间_第四节 线性方程组解的结构_3.4线性方程组解的结构.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-2行列式的性质.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-3行列式的计算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第一章 1-4克拉默法则.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-4矩阵的秩.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-1矩阵的运算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-2逆矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-3初等矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第三章 3-4分块矩阵.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-1消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-2向量及其线性运算.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第二章 2-3向量组的线性关系.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-1线性方程组有解的判定.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-2齐次线性方程组.pdf
- 《线性代数》课程教学资源(课件讲稿,C)第四章 4-3非齐次线性方程组.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-九年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-九年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-七年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-七年级-下.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-八年级-上.pdf
- 《数学教学论》课程教学资源(书籍教材)初中数学教材(五四制)人教版(2012)_人教版-八年级-下.pdf
