《高等数学》课程教学资源（课件讲稿）第二章_2.1 导数的概念

第二章导数与微分微积分学的创始人：英国数学家Newton德国教学家 Leibniz导数— 描述函数变化快慢微分学微分一描述函数变化程度都是描述物质运动的工具(从微观上研究函数)

微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具(从微观上研究函数) 第二章导数与微分 英国数学家 Newton

① 2. 1 导数的概念①2.2函数的求导法则①2. 3隐函数及由参数方程确定的函数求导①2.4函数的微分

Ø 2.1 导数的概念 Ø 2.2 函数的求导法则 Ø 2.3隐函数及由参数方程确定的函数求导 Ø 2.4 函数的微分

2. 1 导数的概念① 一、历史背景① 二、 导数的定义① 三、 导数的几何意义口 四、可导与连续的关系

Ø 一、历史背景 Ø 二、导数的定义 Ø 三、导数的几何意义 Ø 四、可导与连续的关系 2.1 导数的概念

一、历史背景①十七世纪以来，光学透镜的设计以及炮弹轨迹的计算促使欧洲的数学家对曲线的切线进行研究；①牛顿在1761年所著《留数法和无穷级数》一书中提出的中心问题是：已知连续运动的路径，求给定时刻的速度业牛顿（1643-1727）费马（1601-1665）

一、历史背景 Ø牛顿在1761年所著《留数法和无穷级数》一书中提出的中心问题是： 已知连续运动的路径，求给定时刻的速度. Ø十七世纪以来，光学透镜的设计以及炮弹轨迹的计算促使欧洲的数 学家对曲线的切线进行研究；

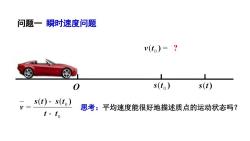
问题一瞬时速度问题v(t.) =Hs(t)s(to)0s(t) - s(to)思考：平均速度能很好地描述质点的运动状态吗？Vt- to

问题一 瞬时速度问题 思考：平均速度能很好地描述质点的运动状态吗？

实例1已知跳水运动员在跳水过程中距离水面高度h与时间t的函数为h(t)= - 4t2 +6t+10经计算可得，从0到1.5秒的平均速度为h(1.5) - h(0)V:=01.5平均速度为0，这显然不能很好地描述跳水运动员的实际运动情况

实例1 已知跳水运动员在跳水过程中距离水面高度h 与时间t 的函数为 经计算可得，从0到1.5秒的平均速度为 平均速度为0，这显然不能很好地描述跳水运动员的实际运动情况。 =0

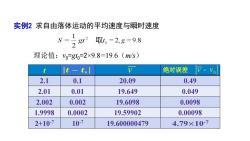
实例2求自由落体运动的平均速度与瞬时速度12812S取t。= 2,g = 9.8理论值：Vo=gto=2×9.8=19.6（m/s）V- Vo绝对误差It-t.lt2.10.120.090.492.010.0119.6490.0492.0020.00219.60980.00981.99980.000219.599020.0009810-72+10-74.79×10-719.600000479

实例2 求自由落体运动的平均速度与瞬时速度 t 2.1 0.1 20.09 2.01 0.01 19.649 2.002 0.002 19.6098 1.9998 0.0002 19.59902 2+10-7 10-7 19.600000479 绝对误差 0.49 0.049 0.0098 0.00098 理论值：v0=gt0=2×9.8=19.6（m/s）

s(t) - s(to)limt?tot-to11CSgto22用平均速度的极限值描述瞬时速度= limtRtot-to1t0limo02tRtot- togto4

用平均速度的极限值描述瞬时速度

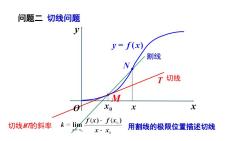
问题二切线问题yy = f(x)割线N切线TMxoxxf(x)- f(x。)k =lim切线MT的斜率用割线的极限位置描述切线YRXOx-Xo

割线 切线 用割线的极限位置描述切线 问题二 切线问题 切线MT的斜率

瞬时速度切线斜率s(t) - s(to)f(x)- f(x。)k=limv =limt?tox?xot- tox- Xo两个问题的共性：所求量为函数增量与自变量增量比值的极限一—-变化率

两个问题的共性 : 瞬时速度 切线斜率 所求量为函数增量与自变量增量比值的极限 -变化率