《高等数学》课程教学资源（课件讲稿）第五章_5.3 定积分的换元积分法

5.3定积分的换元积分法定积分的换元积分法

定积分的换元积分法 1 5.3 定积分的换元积分法

OA0定积分的换元积分法如果函数y=f(x)在区间「a.bl上连续，函数x=i（t)满足条件定理5.4(l)当ti [α,bl(或[b,al)时，afj()ft（2）i（)在区间[α,bl（或[b,a）上有连续的导数，且idt)1c(3)j(a)=α,j(b)=b则有定积分换元公式0 f(x)dx =o fG (0)i d0)dt

定积分的换元积分法 2 定理5.4

A定积分的换元积分法注:定理5.4中的公式从左往右相当于不定积分的第二换元法，从右往左相当于不定积分中的第一换元法（此时可以不换元，而直接凑微分）：与不定积分换元法不同，定积分在换元后不需要还原，只要把最终的数值计算出来即可采用换元法计算定积分时，如果换元，“一定换限；不换元就不换限

定积分的换元积分法 3 定理5.4中的公式从左往右相当于不定积分的第二换元法，从右 往左相当于不定积分中的第一换元法（此时可以不换元，而直 接凑微分）. 与不定积分换元法不同， 定积分在换元后不需要还原，只要把 最终的数值计算出来即可 采用换元法计算定积分时，如果换元，一定换限；不换元就不 换限. 1 2 3

K谷定积分的换元积分法例计算下列定积分(2x - 1)2022 dx:1

计算下列定积分 定积分的换元积分法 4 例 1

?谷定积分的换元积分法1dxdx

定积分的换元积分法 5

O#A定积分的换元积分法求定积分Vsinx-sinxdx.解因为/sinx-sinx=Vsinxcosx=cosx|/sinx，在[0,]上，|cosx=cosx；在「，元]上，|cosx=-cosx.于是Vsin x- sin'xdx=lcosx/Vsin xdx=Vsin xdsinx-Vsin xdsinx232322242sin2sin211X3333372

定积分的换元积分法 6 例 2 解

O定积分的换元积分法结论1设函数y=f(x)在区间[-a,a](a>0)上连续，试证：(1 b, f(x)dx = Lf(x)+ f(- x)]dx0，f(x)是奇函数(2 b. f(x)dx =2.f(x)dx,f(x)是偶函数

定积分的换元积分法 7 结论1

OAA定积分的换元积分法结论1设函数y= f(x)在区间[-a,α](α>0)上连续，试证：(1 6, f(x)dx = Lf(x)+ f(- x)]dx0，f(x)是奇函数，(2 6 f(x)dx =)20 f(x)dx,f(x)是偶函数D证（1）因为函数y=f(x)在[-a,a]上连续，所以f(x)dx存在，由定积分积分区间的可加性得. f(x)dx=0. f(x)dx+f(x)dx,对上式中的of(x)dx，设x=-t,则dx=-dt，且当x=-α时，t=a;当x=0时，t=0.于是O. f(x)dx =-O F(-0)dt = f(-1)d = f(-x)dx,所以. f(x)dx =[f(x)- f(x)]dx.8

定积分的换元积分法 8 证 结论1

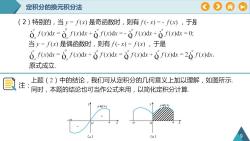
P定积分的换元积分法（2）特别的，当y=f(x)是奇函数时，则有f(-x）)=-f(x），于是0 f(x)dx = 0, f(x)dx + f(x)dx = - f(x)dx + f(x)dx = 0;当y=f(x)是偶函数时，则有f(-x)=f(x），于是O, f(x)dx = 0. f(x)dx + 0 f(x)dx = f(x)dx + 0 f(x)dx = 20 f(x)dx.原式成立上题（2）中的结论，我们可从定积分的几何意义上加以理解，如图所示注同时，本题的结论也可当作公式来用，以简化定积分计算(a)(b)

定积分的换元积分法 9 y=f( x) y y O a x O x y=f( x) + - a - a - a （a） （b）

OA定积分的换元积分法7+sinx求定积分X1+ x2sin x+sinx其中前者是[-1,1]上的偶函数解1 + x21+ x?1+x后者是[-1,1]上的奇函数。于是中I x? +sinxsinxix+0O1+X1+--)dx = 2[x - arctan x]

定积分的换元积分法 10 解 例 3