《高等数学》课程教学资源（课件讲稿）第五章_5.2微积分基本公式

第二节微积分基本公式问题的提出二、积分上限函数及其导数三、牛顿一菜布尼茨公式四、小结

第二节 微积分基本公式 • 一、问题的提出 • 二、积分上限函数及其导数 • 三、牛顿—莱布尼茨公式 • 四、小结

问题的提出一、变速直线运动中位置函数与速度函数的关系设某物体作直线运动，已知速度v=v(t)是[T,T,]上的一个连续函数，且v(t)≥ 0，s= s(t)是位置函数，求物体在这段时间内所经过的路程v(t)dt变速直线运动中路程为另一方面这段路程可表示为 s(T)一S(T)v(t)dt = s(T,)-s(T). 其中 s'(t)= v(t)一般的，设f(x)在[a,b]连续，且 F'(x)=f(x).J' f(x)dx?F(b) -F(a)

变速直线运动中位置函数与速度函数的关系 变速直线运动中路程为  2 1 ( ) T T v t dt 另一方面这段路程可表示为 ( ) ( ) 2 T1 s T − s F x f x ( ) ( ). = ( ) ( ) ( ). 2 1 2 1 v t dt s T s T T T  = −  其中 s(t) = v(t). 一般的，设f(x)在[a,b]连续，且 ( ) ( ) ( ). b a f x dx F b F a = −  一、问题的提出 1 2 ( ) [ , ] ( ) 0 ( ) v v t T T t v t s s t =  = 设某物体作直线运动，已知速度 是 上 的一个连续函数，且 ， 是位置函 数，求物体在这段时间内所经过的路程

二、积分上限函数及其导数设函数f(x)在区间[a,b]上连续，并且设x为[a,b]上的一点，在区间[a,x]考察定积分J f(x)dx= J" f(t)dt如果上限x在区间[a,b]上任意变动，则对于每一个取定的x值，定积分有一个对应值，所以它在[a,b]定义了一个函数记@(x)=[ f(t)dt.积分上限函数

 x a f (x)dx  = x a f (t)dt ( ) ( ) . x a  x f t dt = 记  积分上限函数 二、积分上限函数及其导数 ( ) [ , ] [ , ] [ , ] f x a b x a b a x 设函数 在区间 上连续，并且设 为 上的一点，在区间 考察定积分 [ , ] [ , ] x a b x a b 如果上限 在区间 上任意变动，则 对于每一个取定的 值，定积分有一个对 应值，所以它在 定义了一个函数

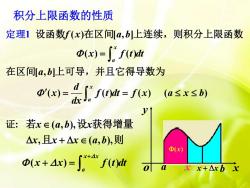
积分上限函数的性质定理1设函数f(x)在区间[a,b]上连续，则积分上限函数Φ(x)= f f(t)dt在区间[a,b]上可导，并且它得导数为d@'(x) =f(t)dt = f(x)(a≤x≤b)dx2yt证：若xE(a,b),设x获得增量Ax,且x + Ar E (a,b),则@(x)x+4x@(x+ 4x) = [x+4f(t)dtolaxx+Axbx

a b x yo 积分上限函数的性质 x + x 证: ( ) ( ) x x a x x f t dt    + + =  (x) x ( , ), , ( , ), x a b x x x x a b   +   若 设 获得增量 且 则 ( ) [ , ] ( ) ( ) [ , ] ( ) ( ) ( ) ) 1 ( x a x a f x a b x f t dt a b d x f t dt f x a x b dx   =  = =     设函数 在区间 上连续，则积分上限函数 在区间 上可导，并且它 为 定 得导数 理

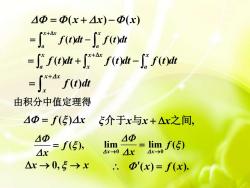
AΦ = Φ(x + 4x)-Φ(x)x+4x-J*+" f(t)dt - f" f(t)dt+A= " f(t)dt + J+*" f(t)dt - J f(t)dtx+4xf(t)dt由积分中值定理得4@ = f()4x介于x与x+△x之间△@4Φlim=lim f(5)= f(5),4x△x4x→04x-→0Ax0,5→x.. @Φ'(x)= f(x)

f t dt f t dt f t dt x a x x x x a   = + − + ( ) ( ) ( ) ( ) x x x f t dt + =  由积分中值定理得    = f x ( ) ξ介于x x x 与 +  之间, x → 0,  → x f ( ), x    = 0 0 lim lim ( ) x x f   x   → →  =  = ( ) ( ). x f x     = + − ( ) ( ) x x x f t dt f t dt x a x x a  = − + ( ) ( )

若x =a,取△r>0，则同理可证Φ(a)= f(a);若x= b,取△x< 0，则同理可证Φ'(b)= f(b)定理2（原函数存在定理）设函数f(x)在区间[a,b|上连续，则积分上限函数Φ(x)=~f(t)dt就是f(x)在区间[a,b)|上的一个原函数定理的重要意义：（1）肯定了连续函数的原函数是存在的（2）初步揭示了积分学中的定积分与原函数之间的联系

定理2（原函数存在定理） 定理的重要意义： （1）肯定了连续函数的原函数是存在的. （2）初步揭示了积分学中的定积分与原函数之 间的联系. ( ) [ , ] ( ) ( ) ( ) [ , ] x a f x a b  x f t dt f x a b =  设函数 在区间 上连续，则积分上限函数 就是 在区间 上的一个原函数. x a x a f a , 0 ( ) ( ) + 若 =    = 取 ，则同理可证  ； x b x b f b , 0 ( ) ( ). − 若 =    = 取 ，则同理可证 

例：求下列函数的导数[,tf(t)dt , xf(t)dt , f*(x-t)f(t)dtso-层ar rom-I roa+()dx补充：如果f(t)连续，a(x)，b(x)可导X则 Fi(x)=Jn*) f(t)dt的导数为F(x)==.(" ()dt = [b(x)1b(x)dx

( ) 1 ( ) ( ) ( ) ( ) ( ) b x a f t a x b x F x f t dt =  如果 连续， ， 可导， 则 的导数为 d ( ) d x a xf t dt x  d ( ( ) ) d x a x f t dt x =  补充: ( ) 1 ( ) ( ) [ ( )] ( ) b x a d F x f t dt f b x b x dx   = =  ( ) , ( ) , ( ) ( ) x x x a a a tf t dt xf t dt x t f t dt −    例：求下列函数的导数 ( ) ( ) x a = + f t dt xf x 

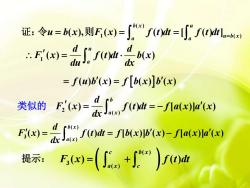
DX证: 令u= b(x),则F;(x)= Jb(") f(t)dt=]" (t)dtlu=b(x)d.. F*(x) = ~J" (t)dt.:b(x)dxd= f(u)b'(x) = f[b(x)]b'(x)F: () - m, (0t= -Ia()2()类似的dcb(x)F'(x) =f(t)dt = f[b(x)]b'(x)- f[a(x)]a'(x)dxJa(x)xF,(x) =( I, + s)提示：f(t)dt

提示： ( ) ( ) 3 ( ) ( ) ( ) c b x a x c F x f t dt = +   ( ) 3 ( ) ( ) ( ) [ ( )] ( ) [ ( )] ( ) b x a x d F x f t dt f b x b x f a x a x dx    = = −  2 ( ) ( ) ( ) [ ( )] ( ) b a x d F x f t dt f a x a x dx  = = −  类似的  1 ( ) ( ) ( ) u a d d F x f t dt b x du dx  =    = = f u b x f b x b x ( ) ( ) ( ) ( )     证： ( ) 1 ( ) ( ), ( ) ( ) [ ( ) ] b x u u b x a a u b x F x f t dt f t dt 令 = = = 则   =

cosx例1 求lim2x-0十这是分析：型不定式，应用洛必达法则0ddecosx解dtdx JidxJcosx.(cosx)' = sinxe-cos*x-cos~xesinx·e-cos'xdtcosx= limlim2x2ex-0x-0

例1 求 lim . 2 1 cos 0 2 x e dt x t x  − → 解  − 1 cos 2 x t e dt dx d , cos 1 2  − = − x t e dt dx d (cos ) 2 cos = −   − e x x sin , 2 cos x x e − =  2 1 cos 0 2 lim x e dt x t x  − → x x e x x 2 sin lim 2 cos 0 − →  = . 2 1 e = 0 0 分析：这是 型不定式，应用洛必达法则

Pus'.arctan(1 + t)dt jdu0lim练习求极限dx-0x(1 - cos x)Cu221xarctan(1 + t)dt JduJo解 原式=2limI-cosx2tx-→02arctan(1 + t)dt= 2lim 0d3x?x-02arctan(1+x) ·2xlim32xx-→02元元634

练习 解 求极限 (1 cos ) [ arctan(1 )d ]d lim 0 0 0 2 x x t t u x u x − +  →       0 0 原式 = 3 0 0 0 [ arctan(1 )d ]d 2lim 2 x t t u x u x  + → 0 2lim → = x 2 1 cos ~ 2 x − x 2 0 arctan(1 )d x + t t  2 3x 0 lim 3 2 → = x 2x arctan(1+ ) 2 x  2x 3 4 6 2   =  =       0 0