《线性代数》课程教学资源（课件讲稿，B）第二章行列式_2-5矩阵的秩

第二章s5矩阵的秩一、矩阵秩的概念二、矩阵秩的计算三、矩阵秩的性质加油！

§5 矩阵的秩 第二章 一、矩阵秩的概念 二、矩阵秩的计算 三、矩阵秩的性质

一、矩阵秩的概念1.定义在 mxn矩阵A中，位于任意确定的k行k列交又点上的k2个元素，按照原来的相对位置组成的阶行列式，称为A的一个k阶子式2取A的第1，2行4和2，4列mxn 矩阵中的k阶子式一共有 Chc(1≤k≤minm,n)加油！

一、矩阵秩的概念 5 2 3 1 4 1 1 7 0 6 2 3 A               取A的第1，2行 和2，4列 2 1   1 7 1.定义 在 矩阵A中，位于任意确定的k行 k列交叉点上的 个元素，按照原来的相对位 置组成的k阶行列式，称为A的一个k阶子式 m n 2 k m n 矩阵中的k阶子式一共有 1 min ,   k k C C k m n m n  

2.矩阵A的秩矩阵中不为零的子式的最高阶数，记为R(A).说明：矩阵A的秩等于r存在不为零的阶子式同时所有的r+1阶子式全部为零加油！

2.矩阵A的秩 矩阵中不为零的子式的最高阶数，记为R(A).    同时所有的  阶子式全部为零 存在不为零的 阶子式 r 1 r 矩阵A的秩等于r  说明：

例求矩阵的秩R(A)=110222R(B)=2(2) B =22C中所有3阶子式全为零，2824(3) C =可得 R(C)= 2.3062加油！

1 1 (1) ; 2 2 248 (2) ; 1 2 1 1 2 4 1 (3) 2 4 8 2 3 6 2 0 A B C                        例 求矩阵的秩 3 ( ) 2. 中所有 阶子式全为零， 可得 C R C  R(A)=1 R(B)=2

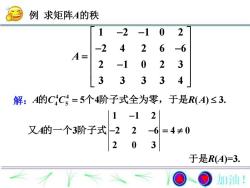
例求矩阵A的秩02-2-11264-6-2A=2032-133334解：A的C4C=5个4阶子式全为零，于是R(A)≤3.21-1 2-6又A的一个3阶子式-2=4±0023于是R(A)=3.加油！

例 求矩阵A的秩 4 4 4 5 A C C R A 的   5 4 ( ) 3. 个 阶子式全为零，于是 于是R(A)=3. 解： 1 2 1 0 2 2 4 2 6 6 2 1 0 2 3 3 3 3 3 4 A                   1 1 2 3 2 2 6 4 0 2 0 3 A  又 的一个 阶子式    

二、矩阵秩的计算定理1初等变换不改变矩阵的秩2例求矩阵的秩 A=2283062解22144100000-10-30所以 R(A) = 2A→0000300-10经行初等变换能将A化为R(A) = r 台纟具有r个非零行的行阶梯形矩阵加油！

定理1 初等变换不改变矩阵的秩。 例 求矩阵的秩 解 所以 R(A) = 2 R(A) = r  经行初等变换能将A化为 具有r个非零行的行阶梯形矩阵. 二、矩阵秩的计算 1 2 4 1 2 4 8 2 3 6 2 0 A            1 2 4 1 0 0 10 3 0 0 0 0              1 2 4 1 0 0 0 0 0 0 10 3 A             

211222设A-已知R(A)=2，求t5t031211解：02424A-6062+t2+t000t=1加油！

  １ ２ １ ２ ２ －２ 设 ＝ ，已知 Ａ ＝２，求ｔ －１ ｔ ５ １ ０ ３ A R             １ ２ １ ０ －２ －４ ０ ２＋ｔ ６ ０ ０ ０ A              解： －２ －４ ＝ ２＋ｔ ６ ｔ＝１

推论A是一个m×n阶矩阵，P,O分别是m阶可逆矩阵和n阶可逆矩阵，则有R(A) = R(PA) = R(PAQ) = R(AQ)3233例 A=0001，求R(AB)2B=000Y加油！

推论 , , A m n P Q m n 是一个  阶矩阵， 分别是 阶可逆矩阵 和 阶可逆矩阵 则有 R A R PA R PAQ R AQ ( ) ( ) ( ) ( )    ,   ３ ４ １ ２ －１ ３ ０ ２ ０ ０ ３ １ ，求 ５ １ ３ ０ ０ ０ A B R AB                       例

矩阵秩的性质1.A为n阶矩阵，则A可逆的充要条件是R(A)=n.2.对任意矩阵A,R(A")= R(A);3.设A为m×n阶矩阵，则0≤R(A)≤min(m,n)[0,k=0,4.对任意矩阵A，R(kA)=R(A), k ± 0.降秩矩阵(满秩矩阵可逆矩阵不可逆矩阵加油！

矩阵秩的性质 0, 0, 4. ( ) ( ), 0. k A R kA R A k       对任意矩阵 ， １. ( ) . A n A R A n 为 阶矩阵，则 可逆的充要条件是  2. ( ) ( ); 对任意矩阵A R A R A ，  T ３. 0 ( ) min( , ); 设A m n R A m n 为    阶矩阵，则 (满秩矩阵——可逆矩阵 降秩矩阵——不可逆矩阵)

R(A)= n,n,例 设A为n阶矩阵(n≥2)，证明 R(A)0, R(A)<n-1.证 ①若R(A)=n: det A=A|+0， AA* =(det A)I =| A|I|A|LAHl(det A)I H|A" 0.所以|A*±0,即R(A*)=n.② R(A)<n-1:A中所有n-1阶子式均为零-R(A*)= 0.-加油！

例 设A为n阶矩阵(n≥2)，证明 证 ①若R(A)=n: det A=|A|≠0， ② R(A) < n-1: A中所有n-1阶子式均为零， * | || | | (det ) | | | 0, n A A A I A    * R A( ) 0.  11 1 * 1 0 0 , 0 0 n n nn A A A A A                       * * 所以 | | 0, ( ) . A R A n   即 * AA A I A I   (det ) | | * , ( ) , ( ) 0, ( ) 1. n R A n R A R A n       