《线性代数》课程教学资源（课件讲稿，B）第四章特征值与特征向量_4-2矩阵的相似对角化

第四章S2矩阵的相似对角化一、相似矩阵的基本概念二、矩阵的相似对角化加油！

§2 矩阵的相似对角化 第四章 一、相似矩阵的基本概念 二、矩阵的相似对角化

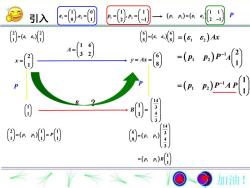
P)=(c)引入82)AxS=(p)p,)P=AxP-IAR2)C)= p(?加油！

引入 2 1 x        6 8 y Ax         1 4 3 2 A        1 2 1 0 , 0 1                 1 2 1 1 , 2 1 p p                 1 2  2 2 1 1                 1 2  6 6 8 8                   1 2  Ax  1 2  2 1 1 1 1 1 p p P                     1 1       B ？ P 14 3 4 3              1 2  14 6 3 8 4 3 p p                     1 2 1 2    1 1 2 1 p p           P P   1 1 2 p p P  2 1 A         1 1 2 p p P A  1 1 B        1 2  1 1 p p B        1 1 P      

一、相似矩阵的基本概念定义设A,B都是n阶矩阵,若有可逆矩阵P使P-1AP=B成立,则A与B相似，记为A～B(1) 反身性A~A;简单性质(2) 对称性A~B则B~A;(3)传递性A~B且B~C则A~C.加油！

1 , , , , ~ . A B n P P AP B A B A B   设 都是 阶矩阵 若有可逆矩阵 使 成立 则 与 相似，记为 定义 一、相似矩阵的基本概念 3 ~ ~ ~ .  传递性 A B B C A C 且 则 2 ~ ~  对称性 A B B A 则 ； 简单性质 1 ~ ;  反身性 A A

定理1 相似矩阵有相同的特征值证： 设A～B,则B=P-AP2I-B=2-P-IAP=p-I(aI -A) P=p-I|[2l - A|P|=[21 - A说明：特征多项式相同的矩阵不一定相似R4:0加油！

定理1 相似矩阵有相同的特征值. 1 P I A P       I A1 A B B P AP ~ ,  设 则    1 1 I B I P AP P I A P           说明：特征多项式相同的矩阵不一定相似 1 0 1 1 = = 0 1 0 1 A B             证：

例九A求Ah设矩阵A～△=证明：设A～△,则存在可逆矩阵P，使得P-1AP=Λ加油！

1 2 ~ , k n A A                  设矩阵 求 例 1 A P P AP ~ , =  证明： 设   则存在可逆矩阵 ，使得

二.矩阵的相似对角化(2)定理222则，，,是A的全部特征值.设矩阵A～△=2a-a-=(a-a)(a-z)...(a-a.)证：[al-a-a.的全部特征值是：，，…，nA与Λ的特征值相同A的全部特征值是：，，，,加油！

二、 矩阵的相似对角化 1 2 ~ n A                  设矩阵 1 2 . 则    ， ， n 是A的全部特征值 定理2 1 2 .  的全部特征值是：   ， ， ，n  A的全部特征值是：   1 2 ， ， ， n           1 2    n  A与的特征值相同 1 2 n I              证：

定理3n阶矩阵A与对角矩阵相似的充分必要条件是A有n个线性无关的特征向量证：充分性　讠设A有n个线性无关的特征向量：P，Pz，,P,Ap, = 2,P, (i=1,2,.*,n)a2令 P=(P, P2, ... ,PnA=则 AP=P△P-1AP= △2A~A=加油！

充分性 设A n 有 个线性无关的特征向量： 定理3 n阶矩阵A与对角矩阵相似的充分必要条件 是A有n个线性无关的特征向量. 1 2 , , , n p p p 1 2 n                  1 2 ~ n A                    1,2, ,  Ap p i n i i i    令 P p p p   1 2 , , , n  1 AP P P AP  则     证：

元2,必要性设P-IAP=Λ=则 AP=P△2令 P=(P，P2，...,Pn(Ap Ap2... Apn)=(αiP 22P2... 2nAp, = 2;P, (i = 1,2,..,n)Pi，P2，Pn是A的n个线性无关的特征向量加油！

 Ap Ap Ap p p p 1 2 1 1 2 2 n n n        1 1 2 n P AP                    必要性 设 则 AP P   令 P p p p   1 2 , , , n   1,2, ,  Ap p i n i i i    1 2 , , , n p p p 是A n 的 个线性无关的特征向量

3-1求A100例若A=a-12-31解：A的特征多项式为|aI-A(2-2)(2-4)2-3→A的特征值为,=2，=4对 = 2,2-3x,(2I - A)x =2-3X加油！

1 2    A的特征值为  2, 4 解：A的特征多项式为 100 3 1 1 3 A A          例 若 ，求 3 1 1 3 I A           ( 2)( 4)   1 2 1 1 1 1 x x               1 2 2 3 1 (2 ) 1 2 3 x I A x x                2, 对1 

=→基础解系:P=(1,1),：P =(1,1)r为属于特征值2的一个特征向量同理可求属于 ,=4的一个特征向量为 P,=(-1,1)201其中P存在可逆阵P.使P-1AP0A-117022上式改写为其中P-A112.2加油！

2 2 4 ( 1,1) , T 同理可求属于     的一个特征向量为 p 1 : (1 1)T   基础解系 p ， ， 1 (1, 1) 2 , T   p 为属于特征值 的一个特征向量 存在可逆阵P,使 1 2 0 1 1 0 4 1 1 P AP P                 其中 上式改写为 1 1 1 1 2 0 2 2 0 4 1 1 2 2 A P P P                       其中