《高等数学》课程教学资源（课件讲稿）第一章_1.5.4

第八节闭区间上连续函数的性质最大值最小值定理与有界性「i零点定理与介值定理三、小结思考题高等数学（上册）

一 、最大值最小值定理与有界性 二、零点定理与介值定理 三、小结 思考题 第八节 闭区间上连续 函数的性质

一、最大值和最小值定理与有界性定义：对于在区间I上有定义的函数,f(x)如果有 xεI,使得对于任一xEI都有f(x)≤ f(x)(f(x) ≥ f(xo))则称f(x)是函数f(x)在区间I上的最大(小)值例如,J=1 + sinx，,在[0,2元]上,ymax =2, Jmin = 0;y=sgnx,在(-o0,+o0)上, max =1, ymin = -1;当x>0?当x=0在(0,+o0)上，Jmax = ymin = 1.0y=sgnx=3当x<0-1高等数学（上册）

一、最大值和最小值定理与有界性 定义: 0 0 0 0 ( ) ( ) ( ), , ( ( ) ( )) ( ) ( ) ( ) . I f x x I x I f x f f x f x f x f x I x     对于在区间 上有定义的函数 如果有 使得对于任一 都有 则称 是函数 在区间 上的最大 小 值 例如, y  sgnx,在(,)上, 2, ymax  1; ymin   在(0,)上, 1. ymax  ymin  y  1  sin x, 在[0,2]上, 0; ymin  1, ymax            1 0 0 0 1 0 sgn x x x y x 当 当 当

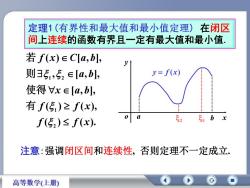
在闭区定理1（有界性和最大值和最小值定理）间上连续的函数有界且一定有最大值和最小值若 f(x) E C[a,b],Jy= f(x)则3,5, E[a,b],使得Vx E[a,b],有 f(S)≥ f(x),aS051bxf(52)≤ f(x)注意：强调闭区间和连续性，否则定理不一定成立高等数学（上册）

定理1(有界性和最大值和最小值定理) 在闭区 间上连续的函数有界且一定有最大值和最小值. a  2 1 b x y o y  f ( x) ( ) ( ). ( ) ( ), [ , ], , [ , ], ( ) [ , ], 2 1 1 2 f f x f f x x a b a b f x C a b            有 使得 则 若 注意:强调闭区间和连续性, 否则定理不一定成立

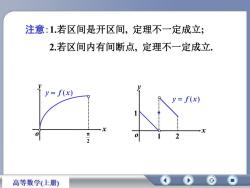
注意：1.若区间是开区间，定理不一定成立;2.若区间内有间断点，定理不一定成立y= f(x)y= f(x)...................xx0元0212高等数学（上册）

x y o y  f ( x) 1 2 1 x y o 2  y  f ( x) 注意:1.若区间是开区间, 定理不一定成立; 2.若区间内有间断点, 定理不一定成立

二、零点定理与介值定理定义：1如果 x使 f(x)=0，则 x。称为函数f(x)的零点.a,b设函数f(x)在闭区间定理2（零点定理）上连续，且f（a）与f(b）异号（即f（a）·f(b）<0那么在开区间(a，b）内至少有函数f(x）的一个零点，即至少有一点(a<<b)，使f()=0.即方程f(x)=0在(a,b)内至少存在一个实根：高等数学（上册）

二、零点定理与介值定理 定义: ( ) . ( ) 0 , 0 0 0 的零点 如果 使 则 称为函数 f x x f x  x 即方程 f (x)  0在(a,b)内至少存在一个实根

几何解释：y=f(x)连续曲线弧y=f(x)的两个0t3aVbxE端点位于x轴的不同侧,则曲线弧与x轴至少有一个交点定理4（介值定理）设函数f(x)在闭区间a,b上连续，且在这区间的端点取不同的函数值f(a)=A 及 f(b)=B,那么，对于A与B之间的任意一个数C，在开区间(a,b)内至少有一点，使得f()=C(a<E<b)高等数学（上册）

a 1  2  3 b 几何解释: . , ( ) 线弧与 轴至少有一个交点 端点位于 轴的不同侧 则曲 连续曲线弧 的两个 x x y  f x x yo y  f (x)

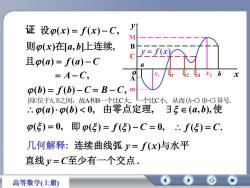
y证 设p(x)= f(x)-C,M则β(x)在[a,b]|上连续BV=C且β(a) = f(a) -C0S5 3 2 b 士x=A-C,Ap(b) = f(b)-C= B-C,m因C位于A，B之间，故A和B一个比C大个比C小，从而（A-C）（B-C)异号:. Φ(a)·Φ(b)<0,由零点定理，日 (a,b),使() = 0, 即 β() = f()-C = 0, : f()=C.几何解释：连续曲线弧y=f(x)与水平直线y=C至少有一个交点.高等数学（上册）

几何解释: M B C A m a x1 1 2 3 x2 b x y o y  f (x) 证 设(x)  f (x)  C, 则(x)在[a,b]上连续, 且(a)  f (a)  C  A  C, (b)  f (b)  C  B  C, (a)(b)  0, 由零点定理,    (a,b),使 ( )  0, 即( )  f ( )  C  0,  f ( )  C. . ( ) 直线 至少有一个交点 连续曲线弧 与水平 y C y f x   因C位于A,B之间，故A和B一个比C大, 一个比C小, 从而(A-C)(B-C)异号

推论在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值例1 证明方程x3－4x2+1=0在区间[0,1]内至少有一根证 令 f(x)= x3 -4x2 +1，则f(x)在[0,1]上连续又 f(0)=1> 0, f(1) =-2<0,由零点定理(a,b), 使f()=0, 即3-4+1=0:方程x3-4x2+1=0在[0,1]内至少有一根三高等数学（上册）

推论 在闭区间上连续的函数必取得介于最大 值 与最小值 之间的任何值. 例1 3 2 4 1 0 [0,1] . 证明方程 x  x   在区间 内 至少有一根 证 ( ) 4 1, 3 2 令 f x  x  x  则f (x)在[0,1]上连续, 又 f (0)  1  0, f (1)  2  0, 由零点定理,    (a,b), 使 f ( )  0, 4 1 0, 3 2 即     3 2 方程x  4x 1 0在[0,1]内至少有一根. M m

例2 设函数 f(x)在区间[a,b]上连续，且f(a)b. 证明3 (a,b), 使得 f()=.证 令 F(x)= f(x)-x，则F(x)在[a,b]上连续,而 F(a) = f(a)-a 0,(a,b), 使 F()= f()-=0,即 f()=5.高等数学（上册）

例2 ( ) . ( , ), ( ) . ( ) [ , ] , ( ) ,        f b b a b f f x a b f a a 证明 使得 设函数 在区间 上连续 且 证 令 F( x)  f ( x)  x, 则F(x)在[a,b]上连续, 而 F(a)  f (a)  a 0, 由零点定理,    (a,b), 使 F( )  f ( )    0, F(b)  f (b)  b  0, 即 f ( )  

三、小结思考题三个定理有界性与最值定理；根的存在性定理；介值定理注意条件　1．闭区间；2．连续函数，这两点不满足上述定理不一定成立解题思路1.直接法：先利用最值定理，再利用介值定理：2.辅助函数法：先作辅助函数F(x),再利用零点定理高等数学（上册）

三、小结 思考题 三个定理 有界性与最值定理；根的存在性定理；介值定理. 注意条件 1．闭区间； 2．连续函数． 这两点不满足上述定理不一定成立． 解题思路 1.直接法:先利用最值定理,再利用介值定理; 2.辅助函数法:先作辅助函数F(x),再利用零点定理;