《高等数学》课程教学资源（课件讲稿）第三章_第三章章习题课

第四章中值定理与导数的应用习题课主要内容典型例题高等数学（上册）

主要内容 典型例题 第四章 中值定理与导数的应用 习 题 课

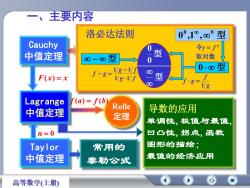
一、主要内容洛必达法则0°,1°,80°型Cauchy令y=f80型-0中值定理取对数8-8型0.8型I-8 -V8型F(x)= xf·g81/9r(a)= f(bLagrangeRolle导数的应用中值定理定理单调性，极值与最值凹凸性，拐点，函数n=0图形的描绘；Taylor常用的最值的经济应用中值定理泰勒公式高等数学（上册）

洛必达法则 Rolle 定理 Lagrange 中值定理 常用的 泰勒公式 0 0 ,1  , 0 型    型 0   型 型 0 0 型   Cauchy 中值定理 Taylor 中值定理 F(x)  x f (a)  f (b) n  0 g f f g 1   g f g f f g 1 1 1 1    取对数 令 g y  f 单调性,极值与最值, 凹凸性,拐点,函数 图形的描绘; 最值的经济应用 导数的应用 一、主要内容

习题课第三章微分中值定理与导数的应用1.微分中值定理及其相互关系f(a)= f(b)拉格朗门中值定理罗尔定理f(b)- f(a)f()= 0F'(5)= sb-aF(x)= xF(x)= xn=0f(a) = f(b)柯西中值定理泰勒中值定理f(b)-f(a) - f'()f(x)= f(xo)+ f'(xo)(x - xo)F(b)-F(a)F'(é)(n)(x)(x - x0)"'(E)(x -x0)n+1+（n+l)高等数学（上册）

3 f (a)  f (b) 1.微分中值定理及其相互关系 罗尔定理 f ( )  0 ( ) ( ) ( ) ( ) ( ) ( )   F f F b F a f b f a      拉格朗日中值定理 ( ) ( ) ( ) f a f b F x x   1 0 ( 1)( )( ) ( 1)! 1      n n f x x n  柯西中值定理 F(x)  x 泰勒中值定理 n n f x x x n ( )( ) ! 1 0 0 ( )   第三章 微分中值定理与导数的应用 习题课 b a f b f a f     ( ) ( ) ( ) ( ) ( ) ( )( ) 0 0 0 f x  f x  f  x x  x n  0

1.罗尔中值定理罗尔（Rolle）定理如果函数f(x）在闭区间[a,bl上连续，在开区间(a,b)内可导，且在区间端点的函数值相等，即f(a)=f(b),那末在(a,b)内至少有一点(a<E<b),使得函数f(x)在该点的导数等于零即f()=0高等数学（上册）

1. 罗尔中值定理 罗尔（Rolle）定理 如果函数f (x)在闭区间 [a,b]上连续,在开区间(a,b)内可导,且在区间端 点的函数值相等，即 f (a)  f (b),那末在(a,b) 内至少有一点(a    b),使得函数f (x)在该 点的导数等于零， 即 ( ) 0 ' f  

2.拉格朗日中值定理拉格朗日（Lagrange）中值定理如果函数f(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，那未在(a,b)内至少有一点(a<<b)，使等式f(b)- f(a)= f ()(b-a) 成立有限增量公式(0 <0 <1)Ay = f'(x, + x).Ax增量△y的精确表达式高等数学（上册）

2. 拉格朗日中值定理 拉格朗日（Lagrange）中值定理 如果函数f (x) 在闭区间[a,b]上连续,在开区间(a,b)内可导,那 末在(a,b)内至少有一点(a    b)，使等式 ( ) ( ) ( )( ) ' f b  f a  f  b  a 成立. ( ) (0 1). y  f  x0 x  x    增量y的精确表达式. 有限增量公式

推论如果函数f(x)在区间I上的导数恒为零,那末f(x)在区间I上是一个常数。3.柯西中值定理柯西（Cauchy）中值定理如果函数f(x)及F(x)在闭区间[a,bl上连续，在开区间(a,b)内可导，且F(x)在(a,b)内每一点处均不为零，那末在(a,b)内至少有一点(a<<b)，使等式-f()f(b) - f(a)成立.F()F(b)- F(a)高等数学（上册）

3. 柯西中值定理 柯西（Cauchy）中值定理 如果函数 f (x)及F(x) 在闭区间[a,b]上连续,在开区间(a,b) 内可导,且 ( ) ' F x 在(a,b)内每一点处均不为零，那末在(a,b) 内至少有一点(a    b),使等式 ( ) ( ) ( ) ( ) ( ) ( ) ' '   F f F b F a f b f a    成立. 推论 ( ) . ( ) , 那末 在区间 上是一个常数 如果函数 在区间 上的导数恒为零 f x I f x I

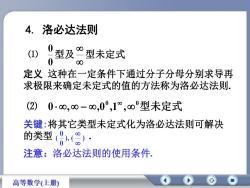
4.洛必达法则8(1)型及=型型未定式08定义这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则(2)0·80,80-80,0°,1°,8°型未定式关键：将其它类型未定式化为洛必达法则可解决的类型(g),(%) .注意：法洛必达法则的使用条件高等数学（上册）

4. 洛必达法则 定义 这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则. ⑴ 型及 型未定式   0 0 ⑵ 0 ,  ,0 0 ,1  , 0型未定式 关键:将其它类型未定式化为洛必达法则可解决 的类型 ), . 0 0 ( ( )   注意：洛必达法则的使用条件

5．泰勒中值定理泰勒（Taylor）中值定理如果函数f(x)在含有x的某个开区间(a,b)内具有直到(n+1)阶的导数则当x在(a,b)内时，f(x)可以表示为(x一x)的一个n次多项式与一个余项R(x)之和：f"(xof(x) = f(xo) + f'(xo)(x -xo) +2!X-x)" + R,(x)n!(n+1) (3)其中 R,(x)(x-x)+1 (在x与x之间)(n + 1)!高等数学（上册）

泰勒(Taylor)中值定理 如果函数 f (x)在含有x0 的某个开区间(a,b)内具有直到(n  1) 阶的导数, 则当 x在(a,b)内时, f (x)可以表示为( ) x  x0 的 一个n次多项式与一个余项R (x) n 之和: ( ) ( ) ! ( ) ( ) 2! ( ) ( ) ( ) ( )( ) 0 0 ( ) 2 0 0 0 0 0 x x R x n f x x x f x f x f x f x x x n n n             5. 泰勒中值定理 ( ) ( ) ( 1)! ( ) ( ) 0 1 0 ( 1) 其中 x x 在 x 与 x 之间 n f R x n n n       

文xer =l+x++0(x")(0<0<1)常用函数的麦克劳林公式2!n!oX+2n+12n+2（-1)sinx = x3!5!2n10xtx.2nxcosx =+4!6!2!(2n)!x2xt1In(1 + x) =-1+00xX23n+111+x+x*+...+x" +o(x")1-xm(m-1)(1+x)m =1+mx+xz2!m(m-1)...(m-n+1)x"Tn!店高等数学（上册）

常用函数的麦克劳林公式 ( ) (2 1)! ( 1) 3! 5! sin 2 2 3 5 2 1           n n n o x n x x x x x  ( ) (2 )! ( 1) 2! 4! 6! cos 1 2 2 4 6 2 n n n o x n x x x x x        ( ) 1 ( 1) 2 3 ln(1 ) 1 2 3 1            n n n o x n x x x x x  1 ( ) 1 1 2 n n x x x o x x         ( ) ! ( 1) ( 1) 2! ( 1) (1 ) 1 2 n n m x o x n m m m n x m m x mx             

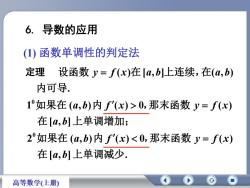
6.导数的应用(1)函数单调性的判定法定理设函数 y= f(x)在[a,b]上连续,在(a,b)内可导。1°如果在(a,b)内 f'(x)>0,那末函数 y= f(x)在[a,bl上单调增加;2°如果在 (a,b)内 f'(x)<0,那末函数 y= f(x)在[a,b]上单调减少。高等数学（上册）

6. 导数的应用 定理 [ , ] . 2 ( , ) ( ) 0 ( ) [ , ] 1 ( , ) ( ) 0 ( ) . ( ) [ , ] ( , ) 0 0 在 上单调减少 如果在 内 ，那末函数 在 上单调增加； 如果在 内 ，那末函数 内可导 设函数 在 上连续，在 a b a b f x y f x a b a b f x y f x y f x a b a b        (1) 函数单调性的判定法